Extremwerte bei Quader, Kugel, Kegel und Zylinder

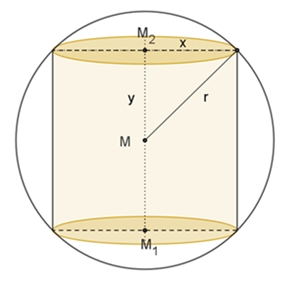
Quader in Kugel

Welcher in eine Kugel einbeschriebene Quader besitzt maximalen Volumeninhalt?

     (2r)² = a² + b² + c² (zweimal Pythagoras)

Volumeninhalt des Quaders V = abc.

Zur Vereinfachung sei c = b und x = a. Dann gilt:

4r² = x² + 2b²   
b = √(2r² – x²/2)

Volumeninhalt des Quaders in Abhängigkeit von x
V(x) = x (2r² – x²/2)
V(x) = 2r²x – x³/2)

V‘(x) = 2r² – 3 x²/2

V‘‘(x) = – 3 x

Bedingung für maximalen Volumeninhalt V‘(x) = 0, daraus folgt:

2r² – 3 x²/2 = 0;  x² = 4/3 r²  ⇨  x = a = 2√3/3 r

b = √(2r² – 2/3 r²);  b = 2√3/3 r ⇨ b = a

V‘‘(2√3/3 r) = – 2√3 r < 0

Aus V‘(x) = 0 und V‘‘(x) < 0 folgt:

Der Volumeninhalt des Quaders wird maximal für a = b = c, d.h. der Quader wird zum Würfel.

Zylinder in Kugel

Wann wird der Volumeninhalt eines in eine Kugel einbeschriebenen Zylinders maximal?

Volumen des Zylinders V =  r_Z²π h, x = r_Z

y = r² – x²  (Pythagoras)

y = √( r² – x²), h = 2y

Volumen des Zylinders in Abhängigkeit von x:

V(x) = x²π⸱2√( r² – x²), x < r

V‘(x) = 2x π (2r² – 3x²) / √( r² - x²)

V‘(x) = 0 für 2r² – 3x² = 0

x = √6/3 r ≈ 0,816 r

V‘‘(x) = 2 π (6x⁴ – 9r²x² +2r⁴) / ( r² – x²)^3/2 

V‘‘(0,816 r) ≈ – 43,5 r < 0

V‘(x) = 0 und V‘‘(x) < 0, daraus folgt:

Der Volumeninhalt des Zylinders wird maximal für x = √6/3 r ≈ 0,816 r.

y = √(r² – 2/3 r²) = √3/3 r ≈ 0,577 r.

Volumeninhalt V_Z des Zylinders V_Z = (√6/3 r)² π⸱2√3/3 r = 4√3/9 r³ π

Volumeninhalt V_K der Kugel V_K = 4/3 r³ π

Volumenverhältnis V_Z : V_K = (4√3/9 r³ π) : (4/3 r³ π) = √3/3 ≈ 0,577 = 57,7%

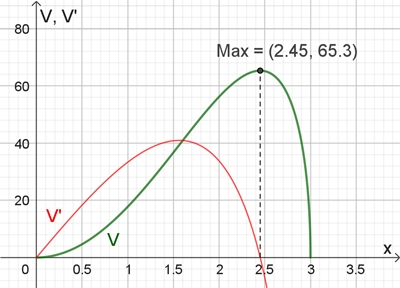
Graphische Darstellung des Volumeninhalts V und V‘ für r = 3

V(x) = x²π٠2√( 9 – x²)

Für x = √6 ≈ 2,45 ist der max. Volumeninhalt des Zylinders V_Z = 12√3 π ≈ 65,3

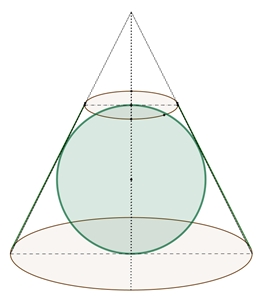
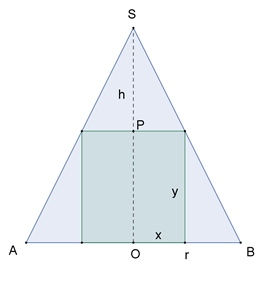
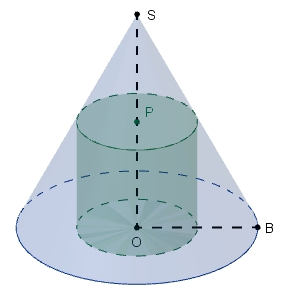
Zylinder im Kegel

Gegeben ist ein Kegel mit dem Radius r und der Höhe h.

Welcher - wie dargestellt - einbeschriebene Zylinder besitzt den größten Volumeninhalt?

y : h = (r – x) : r  (Strahlensatz)

y = (r – x) h / r

Zylindervolumen:

V(x) = x² π (r – x) h / r

V(x) = (r x² – x³) h π / r

V‘(x) = (2r x – 3x²) h π / r

V‘(x) = 0 für 2r x – 3x² = 0 | : x > 0

2r  – 3x = 0 

x = 2/3 r;  y = 1/3 h

V‘‘(x) = (2r  – 6x) h π / r

V‘‘(2/3 r) = – 2 h π < 0

V'(x) = 0 und V''(x) < 0, daraus folgt:

Der Zylinder hat für x = 2/3 r den maximalen Volumeninhalt.

Volumeninhalt V_Z dieses Zylinders V_Z = x² π (r – x) h / r = 4/27 r² π h

Volumeninhalt V_Ke des Kegels V_Ke = 1/3 r² π h

Volumenverhältnis V_Z : V_Ke = (4/27 r² π h) : (1/3 r² π h) = 4/9 ≈ 44,4%

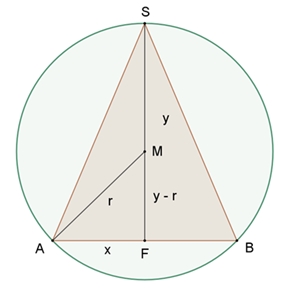
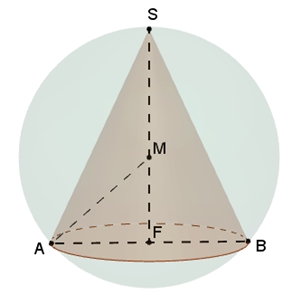
Kegel in Kugel

Ein Kegel soll in eine Kugel mit maximalem Volumeninhalt einbeschrieben werden.

x = Radius des Grundkreises des Kegels, y = Kegelhöhe

(y – r)² = r² – x²  (Pythagoras)

y – r = √( r² – x²), x < r

y = r + √( r² – x²)

Volumeninhalt des Kegels

V(x) = 1/3 x² π (r + √( r² – x²))

V‘(x) = = 1/3 x π (2 r √( r² – x²) – 3 x² + 2 r²) / √( r² – x²)

V‘(x) = 0, daraus folgt:

2 r √( r² – x²) – 3 x² + 2 r² = 0

2 r √( r² – x²) = 3 x² – 2 r²  | □²

4 r² (r² – x²) = 9 x⁴ – 12 r² x² + 4 r⁴

 4 r⁴ – 4 r² x² = 9 x⁴ – 12 r² x² + 4 r⁴  |  – 4 r²

                  0  = 9 x⁴ – 8 r² x²  | : x² > 0

                9 x² = 8 r²

                   x  =  2√2 /3 r ≈ 0,943 r

                   y = r + 1/3 r;  y = 4/3 r

V(2√2 /3 r) = 32/27 r³ π

V‘‘(x) = 1/3 π (2r ( r² – x²)^3/2 + 6 x⁴ – 9 r² x² + 2 r⁴) / ( r² – x²)^3/2

V‘‘(2√2 /3 r) = –32/3 r π < 0

Der Kegel besitzt für x = 2√2 /3 r ≈  0,943 r  maximalen Volumeninhalt.

Volumeninhalt dieses Kegels V_Ke = 32/81 π r³ 

Volumeninhalt der Kugel V_Ku = 4/3 π r³ 

Volumenverhältnis V_Ke : V_Ku = 32/81 ٠ 3/4 = 8/27 ≈ 29,6%

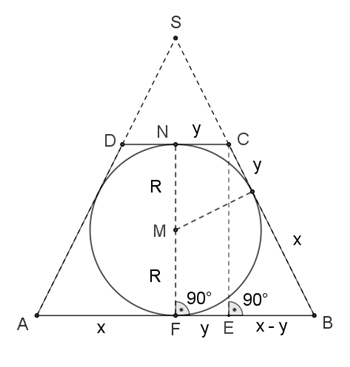
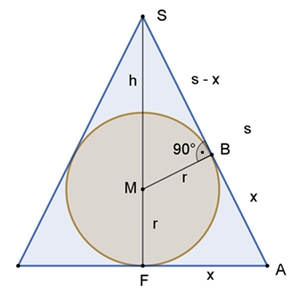
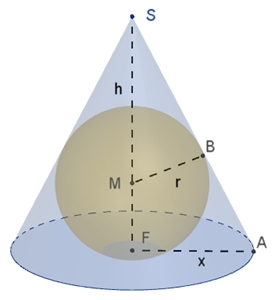
Kegel um Kugel

Wann wird der Volumeninhalt eines Kegels, der einer Kugel umbeschriebenen wird, minimal?

  Es gilt: x > r

s² = h² + x²  (Pythagoras im Dreieck FAS)

s = √( h² + x²)   (1)

(h – r)² = r² + (s – x)²

h² – 2hr =  (s – x)²

√(h² – 2hr) = s – x  (2)

(1) in (2):   √(h² – 2hr) = √( h² + x²)  – x  |  □²

 (h² – 2hr) = ( h² + x²) – 2x√( h² + x²)  + x²  | - h² - 2 x²  | ٠(-1)

  –2x²  – 2hr = – 2x√( h² + x²)  | : ( –2)  |  □²

  (x²  + hr)² = x² ( h² + x²) 

   x⁴  + 2hr x² + h² r² =  h² x² + x⁴  | – x⁴  | : h

  2r x² + h r² =  h x²  | – h r²

   2r x² =  h x² – h r²

         h = 2r x² / (x² – r²)

Damit ergibt sich für den Volumeninhalt V des Kegels in Abhängigkeit von x:

V(x) = 1/3 x² π ⸱ 2r x² / (x² – r²)

V(x) = 2/3 r π  x⁴ / (x² – r²)    

V‘(x) = 4/3 r π  x³ (x² – 2 r²) /  (x² – r²)²

V‘(x) = 0  ⇨  x² – 2 r² = 0;  x = √2 r

V‘‘(x) = 4/3 r π  x² (x⁴ – 3 r² x² + 6 r⁴) / (x² – r²)³ 

V‘‘(√2 r) = 32/3 r π > 0

Der Volumeninhalt des Kegels ist für x = √2 r minimal.

Volumeninhalt des Kegels V_Ke = 8/3 r³ π

Volumeninhalt der Kugel V_Ku = 4/3 r³ π

Volumenverhältnis V_Ke : V_Ku = 2 : 1

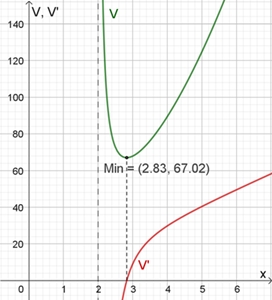
Graphische Darstellung

des Volumeninhalts V des Kegels und V‘ für r = 2

x = 2√2 ≈ 2,83

V(2√2) = 64/3 π ≈ 67,02

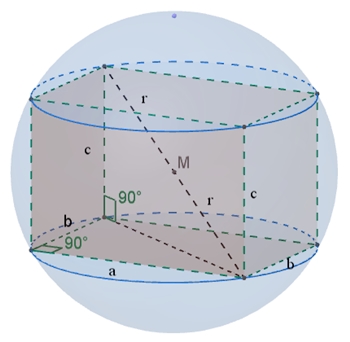
Kugel im Kegelstumpf

Gegeben ist eine Kugel vom Radius r.

Die Kugel sei einem geraden Kegelstumpf einbeschrieben, d.h. sie berührt Grundfläche, Deckfläche und Mantelfläche des Kegelstumpfes.

Wie sind die beiden Radien des Kegelstumpfes zu wählen, damit sein Volumeninhalt minimal wird?

I    V = 2rπ/3 (x² + xy + y²)    (nach Formel)

II   (x + y)² = (x – y)² + (2r)²  (Pythagoras im Dreieck EBC)

       x² + 2xy + y² = x² – 2xy + y²  + 4r²

                     4xy  =  4r²

                          y = r²/x

in I     V(x) = 2rπ/3 (x² + r² + r⁴/x²)

V‘(x) = 2rπ/3 (2x – 2r⁴/x³) 

V‘(x) = 4rπ (x⁴ – r⁴) / (3 x³)

V‘‘(x) = 4rπ (x⁴ – 3r⁴) / (3 x⁴)

V‘(x) = 0, daraus folgt:

(x⁴ – r⁴) = 0

x = r und y = r

V‘‘(r) = 16/3 rπ > 0

V‘(x) = 0 und V‘‘(x) > 0, daraus folgt minimaler Volumeninhalt für x = r.

Der Kegelstumpf wird im Grenzfall zum Zylinder.

Je mehr sich der Kegelstumpf dem Zylinder mit Radius r annähert, umso kleiner wird der Volumeninhalt des Kegelstumpfes.

Zurück
Zurück zur Startseite