Das sphärische Dreieck (Kugeldreieck)

Flächeninhalt des sphärischen Dreiecks

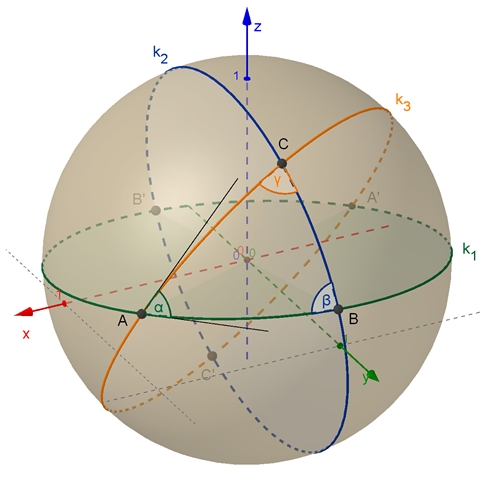
Das sphärische Dreieck wird auf der Kugeloberfläche von drei Großkreisen begrenzt.
Die Mittelpunkte der Großkreise fallen mit dem Mittelpunkt der Kugel überein.
Es werden nur sog. Eulersche Dreiecke betrachtet, deren Innenwinkel kleiner als 180° sind.

Die Winkel α, β und γ des sphärischen Dreiecks ABC sind gegeben durch die Tangenten in den Punkten A, B und C an die Großkreise k₁, k₂ und  k₃.

Der Flächeninhalt des sphärischen Dreiecks beträgt A_ABC = (α + β + γ – π) r²

Begründung: 

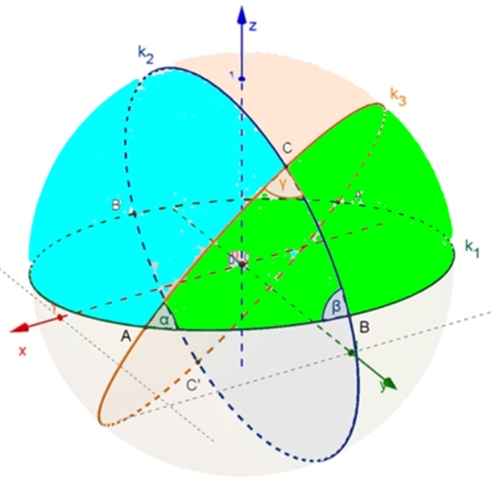
Das Zweieck AA‘ durch B und C besitzt den Flächeninhalt A_α = 2αr².
α : 2π  =  A_α : 4πr²,  daraus folgt:  A_α = 2αr²  ( 360°≙ 2π im Bogenmaß)

Entsprechend gilt:  A_β = 2βr²  und  A_γ = 2γr² (Zweieck CC‘ oberhalb von C mit ΔABC statt ΔA’B’C‘).

Die drei Zweiecke mit den Flächeninhalten  A_α, A_β und A_γ überdecken eine Halbkugeloberfläche, wobei die Fläche des sphärischen Dreiecks A_ABC zusätzlich zweimal überdeckt wird. Der halbe Kugeloberflächeninhalt ist 2πr². Daraus folgt:

2A_ABC = (2αr² + 2βr² + 2γr² – 2πr²)
A_ABC = (α + β + γ – π) r²

Für die Winkelsumme α + β + γ eines sphärischen Eulerschen Dreiecks gilt dann:

α + β + γ = A_ABC / r² + π.

Daraus folgt:  Die Winkelsumme im sphärischen Dreieck ist stets größer als π ≙ 180°.

Der Seitensinussatz des sphärischen Dreiecks

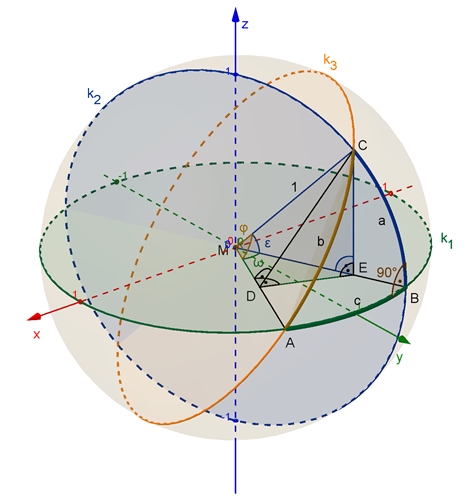
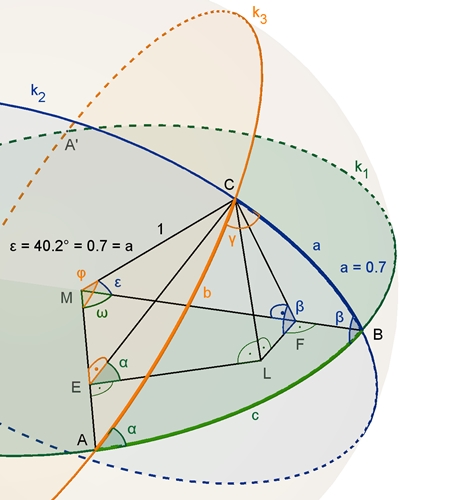
Die Punkte A, B und C liegen auf Großkreisen der Kugeloberfläche und bilden das sphärische Dreieck ABC. Der Radius der Kugel und der Großkreise sei zur Vereinfachung gleich 1.Der Mittelpunktswinkel ε zum Kreisbogen a hat im Bogenmaß den gleichen Wert.
a : 2rπ = ε : 360° mit r = 1 folgt: a ≙ ε (a im Bogenmaß, ε im Gradmaß).

L ist der Lotfußpunkt von C auf die Ebene E(A,B,M), in der der Kreis k₁ liegt.
E ist der Lotfußpunkt von L auf AM und F ist der Lotfußpunkt von l auf BM, wobei gilt: E(E,L,C) ⏊ AM  und  E(F,L,C) ⏊ BM.

Man erhält 2 rechtwinklige Dreiecke ELC und FLC.
|EC| = sin(φ) = sin(b), da im Dreieck MEC  Hypotenuse |MC| = 1.
|FC| = sin(ε) = sin(a), da im Dreieck MFC Hypotenuse |MC| = 1.
Im Dreieck ALC gilt:  |LC| : |EC| = sin(α), mit |EC| = sin(b) folgt: |LC| = sin(α)٠sin(b)  (1).
Im Dreieck FLC gilt:  |LC| : ||FC| = sin(β), mit |FC| = sin(a) folgt: |LC| = sin(β)٠sin(a)  (2).

Aus (2) = (1) folgt:   sin(β)٠sin(a)  = sin(α)٠sin(b)  oder   sin(a) : sin(b) = sin(α) : sin(β).

Entsprechend lässt sich folgern:  sin(b) : sin(c) = sin(β) : sin(γ).

Zusammenfassend gilt der Seitensinussatz:
                         sin(a) : sin(b) : sin(c) = sin(α) : sin(β) : sin(γ).

Der Seitenkosinussatz des sphärischen Dreiecks

GF || EL  und  HL || GE.

|EM| = cos(φ) = cos(b) (1), da im Dreieck MEC Hypotenuse |MC| = 1.
|LF| : |FC| = cos(β), mit |FC| = sin(a) folgt:
|LF| = sin(a)٠cos(β)
|EM| = |EG| + |GM| und |EG| = |LH|
∢ LFH = ∢ AMB = ω, da die Schenkel paarweise aufeinander senkrecht stehen,
|LH| : |LF| = sin(ω) = sin(c), daraus folgt:
|EG| = |LH| = sin(a)٠cos(β)٠sin(c) (2)

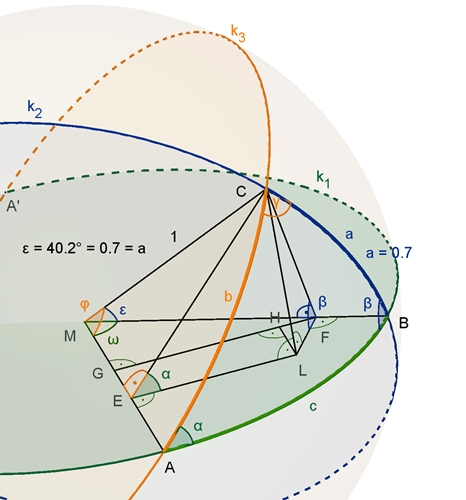
|FM| = cos(ε) = cos(a), da im Dreieck MFC Hypotenuse |MC| = 1, und |GM| : |FM| = cos(ω) = cos(c). Daraus folgt:  |GM| = cos(a)٠cos(c)  (3).

Aus (1), (2) und (3) folgt der Seitenkosinussatz: 

cos(b) = cos(a)٠cos(c) + sin(a)٠sin(c)٠cos(β), und entsprechend hergeleitet
cos(a) = cos(b)٠cos(c) + sin(b)٠sin(c)٠cos(α)
cos(c) = cos(a)٠cos(b) + sin(a)٠sin(b)٠cos(γ)
 

Der Winkelkosinussatz des sphärischen Dreiecks

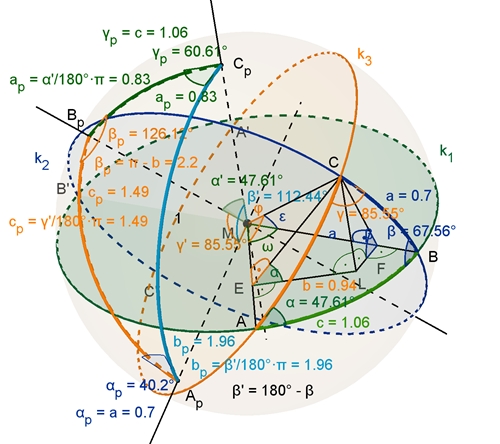
Herleitung des Winkelkosinussatzes mit Hilfe des Polardreiecks:

Das Polardreieck A_pB_pC_p erhält man wenn man die Normalen zu den Großkreisebenen E₁, E₂ und E₃ im Linksdrehsinn mit der Kugeloberfläche schneidet.

Die Mittelpunktswinkel zu den Seiten a_p, b_p und c_p des Polardreiecks seien α‘, β‘ und γ‘. Es gilt:
α‘ = α, γ‘ = γ und β‘ = 180°– β.

a_p = α, c_p = γ, b_p = π – β (Winkel im Bogenmaß) und β_p = π – b.

Einsetzen der Werte für das Polardreieck in den Seitenkosinussatz
cos(b_p) = cos(a_p)٠cos(c_p) + sin(a_p)٠sin(c_p)٠cos(β_p) liefert:

cos(π – β) = cos(α)٠cos(γ) + sin(α٠sin((γ)٠cos(π – b)

– cos(β) = cos(α)٠cos(γ) – sin(α٠sin((γ)٠cos(b)   | ٠(–1)

Ergebnis: Winkelkosinussatz

cos(β) = – cos(α)٠cos(γ) + sin(α٠sin((γ)٠cos(b),   entsprechende Herleitung für

cos(α) = – cos(β)٠cos(γ) + sin(β ٠sin((γ)٠cos(a)  

cos(γ) = – cos(α)٠cos(β) + sin(α ٠sin((β)٠cos(c)  

Die Seitenlängen des sphärischen Dreiecks

Auf einer Kugeloberfläche mit Kugelradius r ist ein sphärisches Dreieck gegeben, deren Seiten Bogen von Großkreisen der Kugel sind. Bei gegebenen Mittelpunktswinkeln zu den Seiten des sphärischen Dreiecks lassen sich die Seitenlängen berechnen:

a = ε/180°٠rπ, b = φ/180°٠rπ und c = ω/180°٠rπ,  (ε, φ und ω im Gradmaß)

Das rechtwinklige sphärische Dreieck

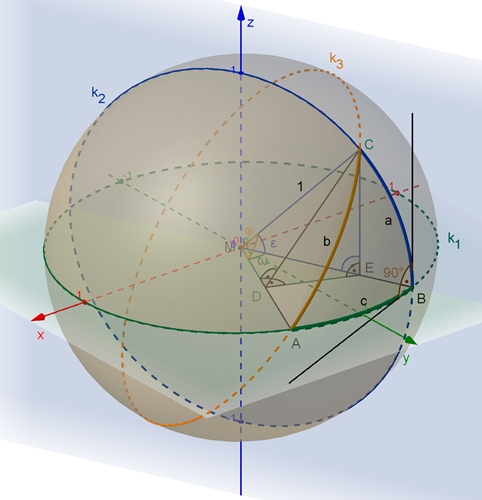
Die Punkte A, B und C liegen auf Großkreisen der Kugeloberfläche und bilden das sphärische Dreieck ABC. Die Mittelpunkte der Großkreise fallen mit dem Mittelpunkt der Kugel – hier im Ursprung des Koordinatensystems – überein.

Die Bogen (Seiten) a, b und c des sphärischen Dreiecks ABC besitzen die Mittelpunktswinkel ε, φ und ω. Für r = 1 gilt:
a : 2π = ε : 360°,  a = ε : 360°٠2π oder  a = ε : 180°٠ π, daraus folgt:
a ≙ ε, b ≙ φ und c ≙ ω (a, b und c im Bogenmaß, ε, φ und ω im Winkelmaß)

Die Großkreise k₁, k₂ und k₃ sind die Schnittkreise der Kugeloberfläche K mit den Ebenen E₁, E₂ und E₃ durch die Punkte A, B, C und Mittelpunt M der Kugel (gleich Ursprung des Koordinatensystems),
k₁ ϵ E₁(A,B,M) = xy-Ebene, k₂ ϵ E₂(B,C,M)⏊ E₁ und k₃ ϵ E₃(A,C,M).

Behauptung:  Mit ∢ CBA = 90° gilt:   cos(a)٠cos(c) = cos(b)

Begründung:

Zur Vereinfachung sei der Radius der Kugel gleich 1.

Im rechtwinkligen Dreieck MDC gilt:  |MD| : |MC| = cos(b) mit |MC| = 1 folgt:
|MD| = cos(b)  (1)

Im rechtwinkligen Dreieck MEC gilt:  |ME| : |MC| = cos(a) mit |MC| = 1 folgt:
|ME| = cos(a)

Im rechtwinkligen Dreieck DEM gilt: 
|MD| : |ME| = cos(c)  mit  |ME| = cos(a)  folgt: |MD| = cos(a)٠cos(c)  (2)

Aus (1) und (2) folgt:  cos(a)٠cos(c) = cos(b)

Entsprechend gilt:

∢ BAC = 90°:   cos(b)٠cos(c) = cos(a)
∢ ACB = 90°:   cos(a)٠cos(b) = cos(c)

Zurück
Zurück zur Startseite