|
Pythagoreische Quadrupel
[a, b, c, d]
mit a² + b² + c²
= d², wobei a, b, c und d
natürliche Zahlen sind.
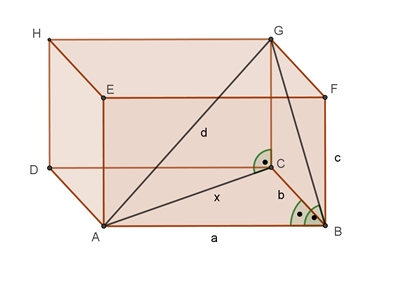
Ein Quader ABCDEFGH veranschaulicht die
Gleichung a² + b² + c² =
d²;
Programm in
der Programmiersprache
Python
ogr = 20
print('Lösungen für a^2 + b^2 + c^2 = d^2')
print('Obergrenze für a, b oder c gleich 20')
print('
a b
c d')
for a in
range(1,ogr+1):
for b in
range(a,ogr+1):
for c in range(b,ogr+1):
p = a*a + b*b + c*c
q = p**(1/2)
d = int(q)
if d*d == p:
print('%4d %4d %4d %4d' % (a,b,c,d))
Lösungen für a^2 + b^2 + c^2 = d^2
Obergrenze für a, b oder c gleich 20
a
b c
d
1
2 2
3
1
4 8
9
1
6 18
19
1
12 12
17
2
3 6
7
2
4 4
6
2
5 14
15
2
6 9
11
2
8 16
18
2
10 11
15
3
4 12
13
3
6 6
9
3
14 18
23
4
4 7
9
4
5 20
21
4
6 12
14
4
8 8
12
4
8 19
21
4
12 18
22
4
13 16
21
5
10 10
15
6
6 7
11
6
6 17
19
6
9 18
21
6
10 15
19
6
12 12
18
6
13 18
23
7
14 14
21
8
8 14
18
8
9 12
17
8
11 16
21
8
16 16
24
9
12 20
25
9
18 18
27
10
20 20
30
12
12 14
22
12
15 16
25
17
20 20
33
Mit folgender Formel lassen sich mit Hilfe
von DERIVE bei gegebener
Differenz
2 (n - 1)·(n + 1) 2 (n - 1)·(n + 1) f(a, n) := [ a, a + n, a + n·a + ———————————————, a + n·a + —————————————— + 1 ] 2 2 z.B. n = 9 VECTOR(f(a,n),a,1,10) 1 10 50 51 2 11 62 63 3 12 76 77 4 13 92 93 5 14 110 111 6 15 130 131 7 16 152 153 8 17 176 177 9 18 202 203 10 19 230 231
Formel für gerade a und gerade n, wobei d – c = 2: 2 2 a n n 2 a n n 2 g(a, n) := [ a, a + n, —— + —·a + ( — ) - 1, —— + —·a + ( — ) + 1 ] 2 2 2 2 2 2
z.B. n
= 8
2 10 25 27 4 12 39 41 6 14 57 59 8 16 79 81
10
18
105
107
12
20
135
137
14
22
169
171
16
24
207
209
18
26
249
251
20
28
295
297
Vielfache einer Lösung sind auch Lösungen, z.B.: h(a) := [a, 2·a, 2·a,
3·a]
VECTOR(h(a), a,
1, 10) 1 2 2 3 2 4 4 6 3 6 6 9 4 8 8 12 5 10 10 15 6 12 12 18 7 14 14 21 8 16 16 24 9 18 18 27 10 20 20 30
Lösungen in Python für primitive
Quadrupel, d.h. a, b und c sind teilerfremd,
a
b c
d
1
2 2
3
1
4 8
9
1
6 18
19
1
12 12
17
2
3 6
7
2
5 14
15
2
6 9
11
2
10 11
15
2
10 25
27
2
14 23
27
3
4 12
13
3
6 22
23
3
14 18
23
3
16 24
29
4
4 7
9
4
5 20
21
4
8 19
21
4
13 16
21
6
6 7
11
6
6 17
19
6
10 15
19
6
13 18
23
6
21 22
31
7
14 22
27
8
9 12
17
8
11 16
21
8
20 25
33
9
12 20
25
. . .
Lösungen für Quadrupel mit a² + b² + c²
= d² mit Tripel
a² + b² = x²,
a
b c
d
3
4 12
13
5
12 84
85
6
8 24
26
7
24 60
65
9
12 20
25
9
12 36
39
12
16 21
29
12
16 48
52
12
16 99
101
15
20 60
65
15
36 52
65
15
36 80
89
16
63 72
97
18
24 40
50
18
24 72
78
21
28 84
91
21
72 100
125
. . .
Lösungen für Quadrupel mit a² + b² + c²
= d² mit Tripel
a² + b² = x² und
b² + c² = y²,
a, b, c, d, x und y sind natürliche
Zahlen.
a
b c
d
264
448 975 1105
264
495 952 1105
357 1276 6960 7085
528
896 1950 2210
528
990 1904 2210
533
756 3360 3485
792 1344 2925 3315
792 1485 2856 3315
819 1680 3740 4181
861 5852 6864 9061
. . .
Zurück Zurück zur Startseite |