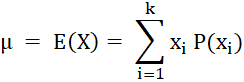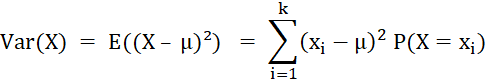|
Zufallsvariablen (Zufallsgrößen)
Definitionen:
Eine Funktion X, die jedem Ergebnis ω einer Ergebnismenge Ω eine reelle Zahl
X(ω) zuordnet, heißt eine
Zufallsvariable X auf Ω. Es
gilt also: X : ω
⟼
X(ω) mit
ω ϵ Ω und
X(ω) ϵ ℝ.
Die Funktion P: x
⟼
P(X = x) mit x ϵ{x1,
x2, x3, …, xk} heißt
Wahrscheinlichkeitsverteilung der
Zufallsvariablen X.
Die Zufallsvariable habe die Wertemenge {x1, x2, x3,
…, xk}. Die zugehörigen Wahrscheinlichkeiten seien P(x1),
P(x2), P(x3), …, P(xk). Dann heißt die Zahl
Die Funktion F: x
⟼
P(X ≤ x) =
X sei eine Zufallsvariable mit der Wertemenge {x1, x2,
x3, …, xk} und E(X) = μ. Dann heißt
Beispiel:
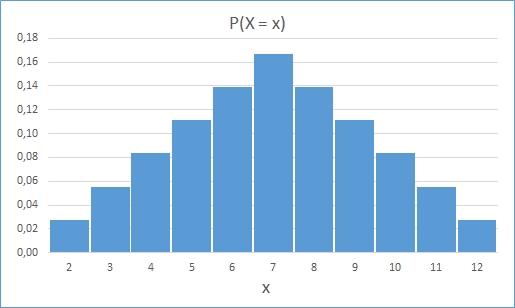
Zweimaliges Werfen eines
Laplace-Würfels mit Notieren der Augensumme als Zufallsvariable X.
Ω = {(1,1),(1,2,), (1,3) …, (6,4), (6,5), (6,6)}, 36 mögliche Ergebnisse ω.
Z.B. werden die Ergebnisse (1,2) und (2,1) der Zahl 3 zugeordnet.
Da alle Würfe gleichwahrscheinlich sind, wird man der Zufallsvariablen X
folgende Wahrscheinlichkeiten zuordnen und erhält als
Wahrscheinlichkeitsverteilung:
Graphische Darstellung als Histogramm (Funktionswerte werden als Balken
dargestellt):
P(X ≤ 4) = 1/36 + 2/36 + 3/36 = 6/36 = 1/6
Der Erwartungswert μ = 2٠1/36 + 3٠2/36
+ … + 11٠2/36 + 12٠1/36
= 7.
Var(X) = (2–7)²٠1/36 + (3–7)²٠2/36
+ … + (12–7)²٠1/36
= 35/6
≈ 5,83
Standardabweichung σ = √5,83 ≈ 2,42
Für die Varianz einer
Zufallsvariablen gilt: σ² =
E(X²) – μ².
Im Beispiel: σ² = 2²٠1/36
+ 3²٠2/36 + … + 12²٠1/36
– 7²
= 329/6 – 49
≈ 5,83
|