Parabel, Kettenlinie und Kreisbogen in Brückenformen

Die Parabel

Funktionsgraph (rot) der Parabel in Scheitelpunktform

Die Parabel ist Graph der quadratischen Funktion mit der Gleichung

I   y = ax² + bx + c, x ∊ ℝ (x ist Element der Menge der reellen Zahlen)

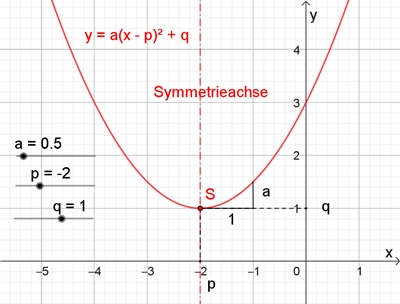
oder in Scheitelpunktform

II  y = a(x – p)² + q, x ∊ ℝ  mit p = – b/(2a), q = c – b²/(4a)

NR: y = a(x² – 2px + p²) + q

        y = ax² – 2apx + ap² + q, durch Vergleich von I und II folgt:

        b =  – 2ap, c = ap² + q, daraus folgt: p = – b/(2a), q = c – b²/(4a) 

Die Kettenlinie

Funktionsgraph (rot) der Kettenlinie, an den Punkten A und B hängend.

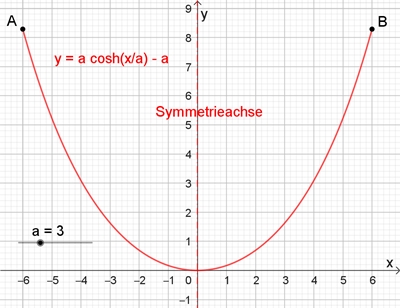
Eine Kettenlinie (Seilkurve) ist eine mathematische Kurve, die den Durchhang einer an ihren Enden aufgehängten Kette unter dem Einfluss der Schwerkraft beschreibt.

Funktionsgleichung:  y = a cosh(x/a) – a, x ∊ ℝ mit dem Parameter a.

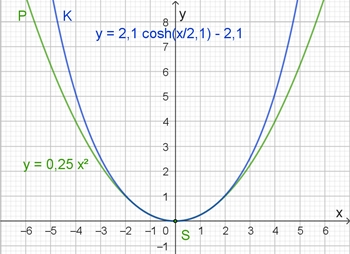
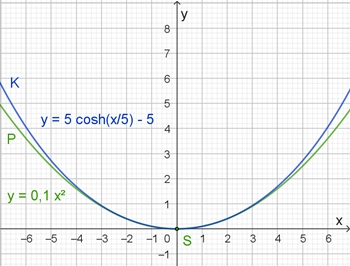
Vergleich von Kettenlinie (blau) und Parabel (grün)

In der näheren Umgebung des Scheitelpunkts S stimmen Parabel und Kettenlinie sehr gut überein. Je flacher Parabel und Kettenlinie sind, um so besser ist die Übereinstimmung in der Umgebung des Scheitelpunkts.

Parabelbogen als Öffnungsform bei Bogenbrücken

Pfaffenberg Brücke Österreich

Eisenbahnbrücke der Tauernbahn als Bogenbrücke aus Stahlbeton mit 200 m Stützweite, Höhe 100 m.

Funktionsgleichung der roten Parabel: y = - 0,0045 x²

x, y in m

Perrine Bridge USA

Fachwerk Bogenbrücke aus Stahl mit einer Spannweite von 303 m,
Höhe 148 m

Funktionsgleichung der roten Parabel: y = – 0,0031 x²  

x, y in m

Wushan-Brücke China

Stahlbetonrohr-Brücke

Spannweite 460 m

Konstruktionshöhe 130 m

Funktionsgleichung der grünen Parabel:  y = - 0,0024 x²

x, y in m

Rundbogen als Öffnungsform bei Bogenbrücken

Steinerne Brücke in Regensburg

Die Steinerne Brücke ist eine Naturstein-Gewölbebrücke mit 16 Segmentbögen, von denen jedoch nur 14 zu sehen sind.

309 m sichtbare Länge, bis 15 m Höhe,
gebaut 1135 – 1146

Der Brückenbogen stimmt erstaunlich gut mit einem Kreisbogen überein.

Kettenlinie als Form des Tragseils einer Hängebrücke

Golden Gate Bridge USA

Gesamtlänge 2,7 km,
längste Stützweite 1280 m, Hängebrückenteil 1970 m, Höhe 227 m, Durchfahrthöhe min. 67 m,

Funktionsgleichung der roten Kettenlinie

y = 1288 cosh(x/1288) – 1288

Funktionsgleichung der blauen Parabel:  y = 0,0004 x²

Die Kurven sind nahezu gleich.

Quellen:

Liste der größten Bogenbrücken – Wikipedia

Liste der längsten Hängebrücken – Wikipedia