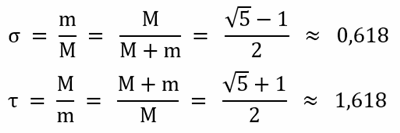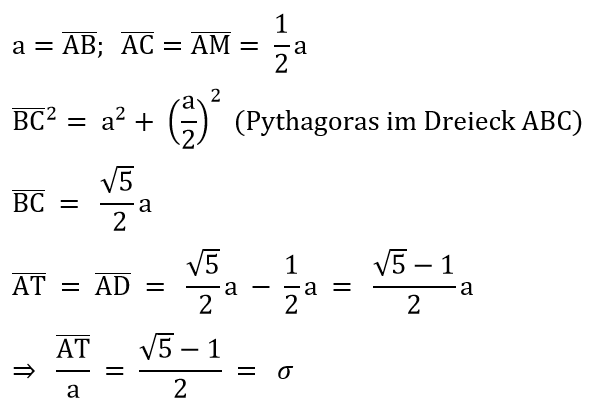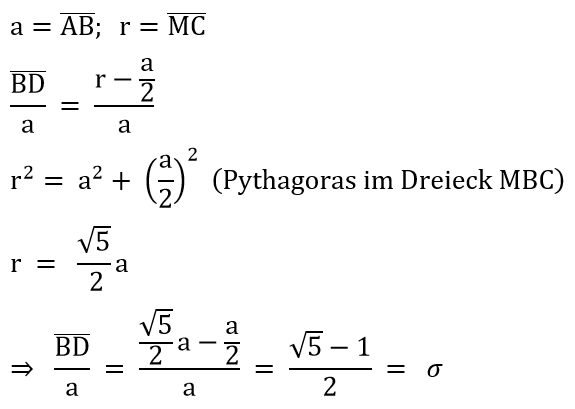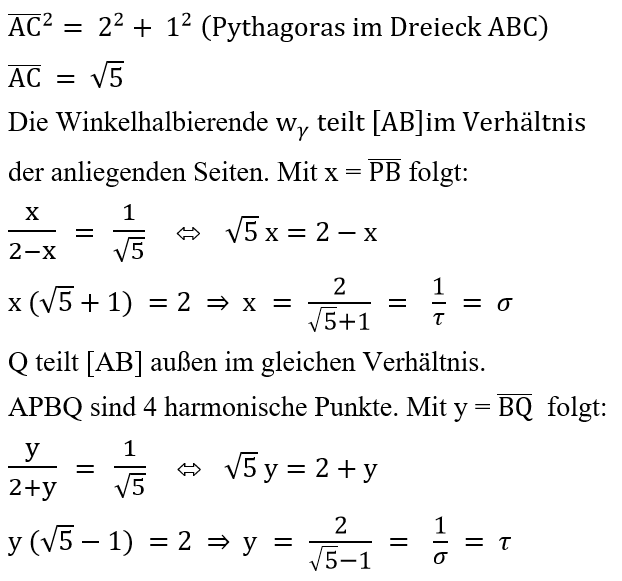Goldener Schnitt – Konstruktionen, VieleckeEs gelten folgende Bezeichnungen und Beziehungen:
An Stelle von τ (tau) wird auch Φ (Phi) verwendet.
σ und τ sind die Zahlen des goldenen
Schnitts.
Von
Johannes Kepler (1571-1630) stammt folgender denkwürdige Satz: Die
Geometrie birgt zwei große Schätze:
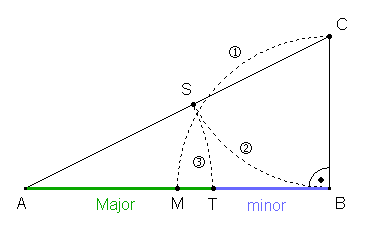
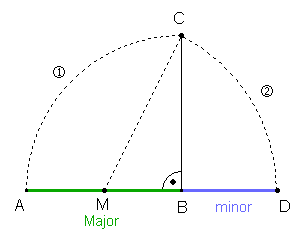
Teilung einer Strecke [AB] im goldenen Schnitt (stetige
Teilung) nach Heron von Alexandria (1 Jh. n. Chr.):
Begründung:
Teilung einer Strecke [AB] im goldenen Schnitt nach
Euklid (3. Jh. v. Chr., Euklid spricht von einer stetig geteilten Strecke):
Begründung:
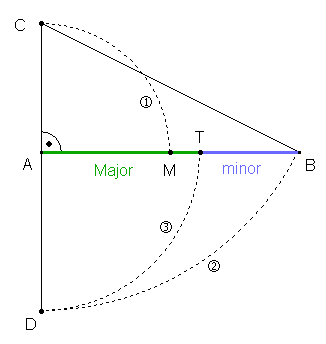
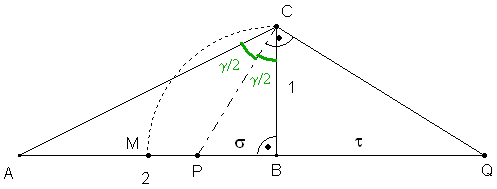
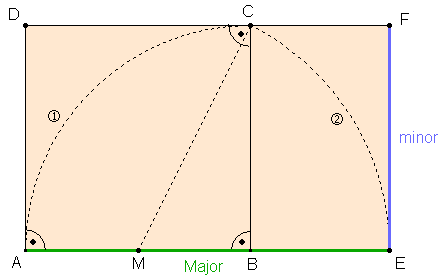
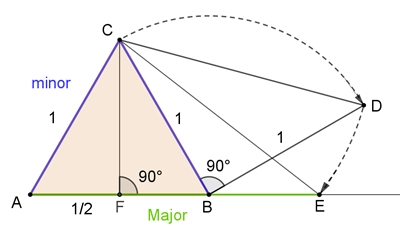
Äußere Teilung einer Strecke [AB] im goldenen Schnitt:
Begründung:
Konstruktion von s und τ :
Begründung:
Konstruktion des goldenen Rechtecks:
AEFD ist ein goldenes Rechteck, BEFC ebenfalls. Konstruktion mit Begründung entsprechend der äußeren Teilung (s.o.).
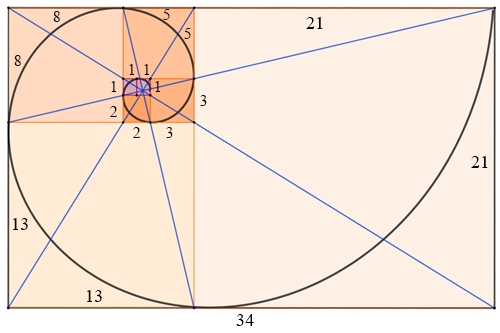
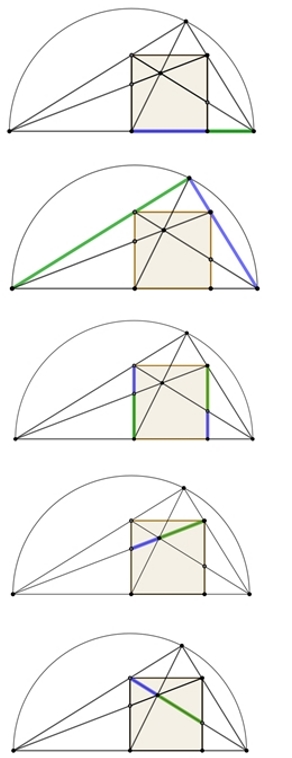
Goldene Spirale durch
ineinandergeschachtelte Quadrate und zunehmend besser genäherte goldene Rechtecke:
Die blauen Linien schneiden sich in genau einem Punkt im
Ausgangsquadrat.
Die goldene Spirale (spezielle logarithmische
Spirale) hat die Funktionsgleichung in
Polarform mit dem Radius r in Abhängigkeit vom Drehwinkel φ:
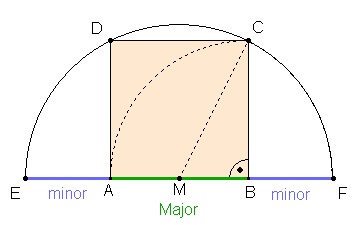
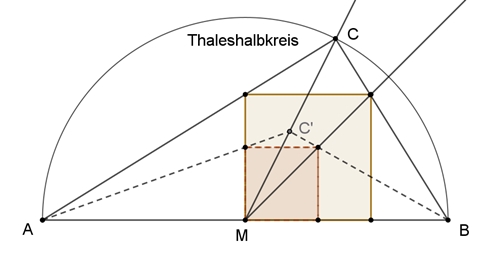
Goldener Schnitt im Halbkreis mit einbeschriebenem
Quadrat:
Konstruktion mit Begründung entsprechend der
äußeren
Teilung (s.o.).
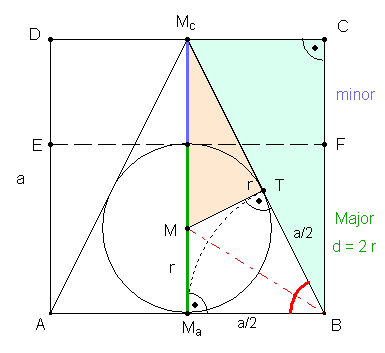
Goldener Schnitt im Quadrat mit gleichschenkligem
Dreieck:
Begründung:
Gleichseitiges Dreieck und goldener
Schnitt
Begründung:
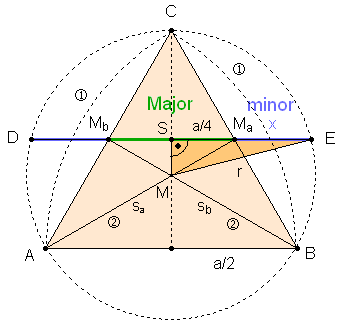
Daraus folgt: Goldener Schnitt im gleichseitigen Dreieck mit Umkreis
von George Odom (1982):
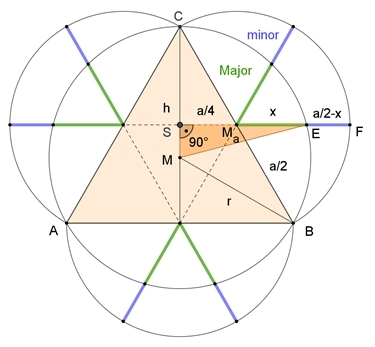
Goldener Schnitt im
gleichseitigen Dreieck mit Möndchen
Begründung:
Nach vorhergehender Figur gilt:
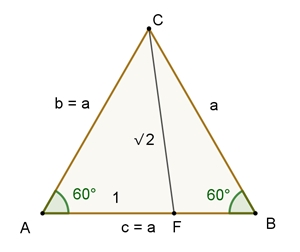
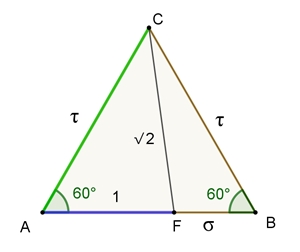
Goldener Schnitt im
gleichseitigen Dreieck mit
√2
Begründung:
Kosinussatz: a² = b² + c² – 2bc
cos(α)
Daraus folgt für das Dreieck AFC: (√2)² = b² + 1² –
2b٠½
b² – b – 1 = 0
b = (1 +
√5)/2 =
τ
≈ 1,618
|AB| =
τ – 1 =
σ
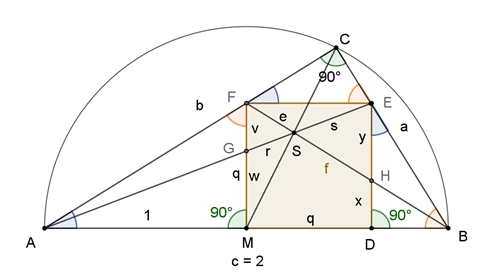
Goldenes rechtwinkliges Dreieck
mit Quadrat
Einem rechtwinkligen Dreieck werde ein Quadrat so einbeschrieben, dass die
linke untere Ecke mit dem Mittelpunkt der Hypotenuse übereinstimmt. Die
Hypotenuse c habe die Seitenlänge 2.
Herleitung der Verhältnisse im
goldenen Schnitt:
△AMF ist ähnlich zu △DBE:
q : 1 = (1 – q) : q
q = (√5 – 1)/2 =
σ
(1 – q)/q =
σ
≈ 0,618
|DB| : |MD| =
σ
△ABC ist ähnlich zu △AMF:
a : b = q : 1 =
σ
≈ 0,618
△DBH ist ähnlich zu △HEF:
x : (1 – q) = (q – x) : q
y = q – x =
(3 – √5)/2
x : y =
= (√5 – 1)/2
=
σ
△GEF ist ähnlich zu △AMG:
v : w = q : 1 =
σ
v berechnen:
v = q – w; w = v/ σ
v = σ – v/ σ
v (1 + σ) = σ2
v = σ2/(1 + σ)
=
√5
– 2
△GSF
ist ähnlich zu
△HES:
v/y = x/y = σ
r : s = v : y = σ
und v : y = r : s = σ
Bemerkung:
Die Verhältnisse gelten
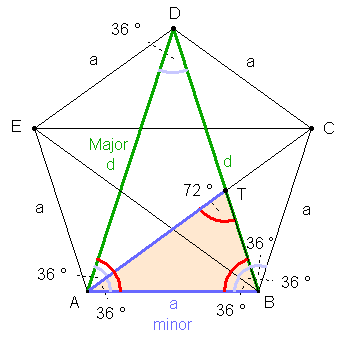
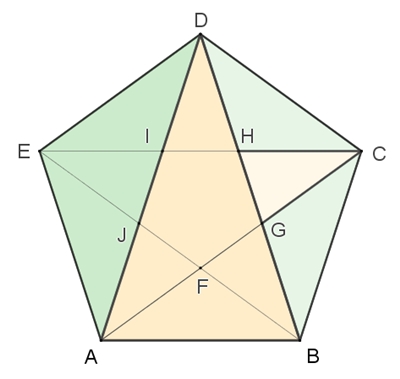
allgemein für beliebiges c. Goldener Schnitt im regelmäßigen Fünfeck:
Begründung:
Die
Innenwinkel des regelmäßigen Fünfecks sind alle gleich groß (540° : 5 =
108°).
Aus
der Kongruenz der Dreiecke ABC, BCD, CDE, DEA und EAB (SWS) folgt,
dass
die Diagonalen im regelmäßigen Fünfeck gleich lang sind.
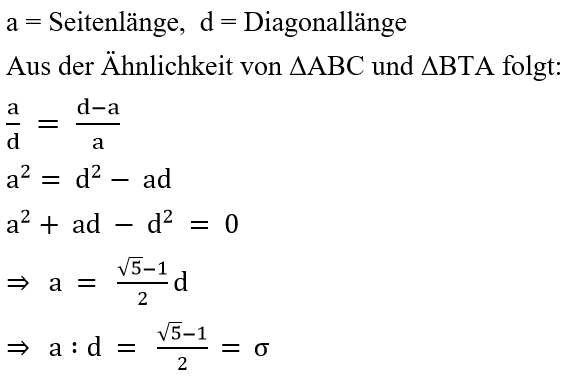
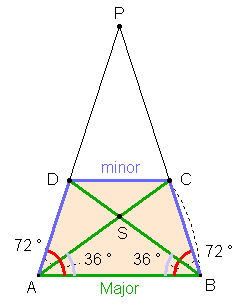
Goldener Schnitt in einer Raute des regelmäßigen
Fünfecks:
Begründung: Die
kongruenten Dreiecke ABC, BCD, CDE usw. sind gleichschenklig und besitzen damit die
Innenwinkel 36°,108° und 36° (Winkelsumme im Dreieck gleich 180°). Über
die Winkel lässt sich folgern, dass das Viereck ABCS ein Parallelogramm mit
gleich langen Seiten sein muss und damit eine Raute darstellt.
Aus
der obigen Begründung folgt ebenfalls: (d - a) : a =
s. Bemerkung: Mathematikprofessor Sir Roger Penrose hat mit dem
konvexen
Drachen ABTS (Kite) und dem
konkaven Drachen STBC (Dart)
als Grundfiguren eine
nichtperiodische Parkettierung der Ebene erzeugt.
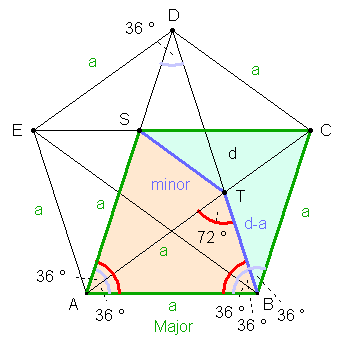
Sinus, Cosinus und die goldenen
Schnittzahlen σ und τ.
a/d = σ
und cos(72°) = a/2 / d, daraus
folgt: cos(72°) = σ/2
d/a = τ
und sin(54°) = d/2 / a,
daraus folgt: sin(54°)
= τ/2 Goldene
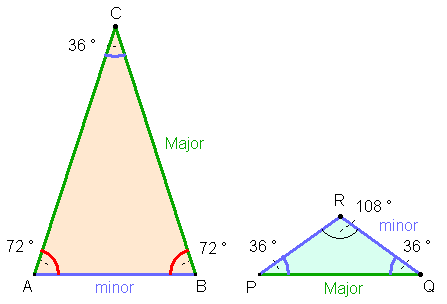
Dreiecke und goldenes Trapez:
Goldene Dreiecke und das goldene Trapez sind im regelmäßigen Fünfeck als Teilfiguren enthalten.
Spitzwinklige goldene
Dreiecke:
Stumpfwinklige goldene Dreiecke:
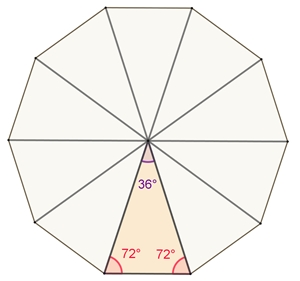
Zehn kongruente spitzwinklige goldene Dreiecke bilden das reguläre Zehneck.
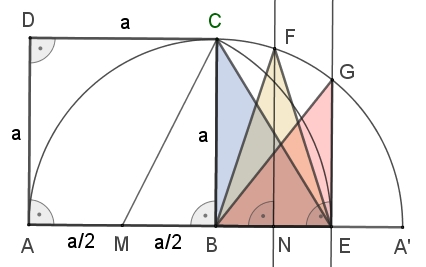
Eudoxos-Dreieck BEC,
Goldenes Dreieck BEF, Kepler-Dreieck BEG
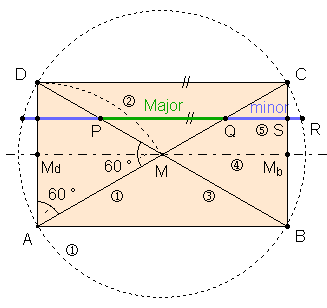
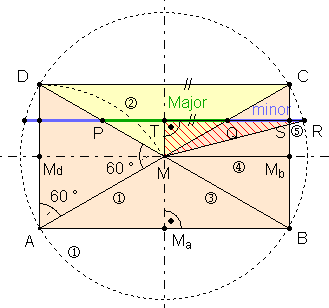
Goldener Schnitt im speziellen Rechteck mit Umkreis:
Begründung:
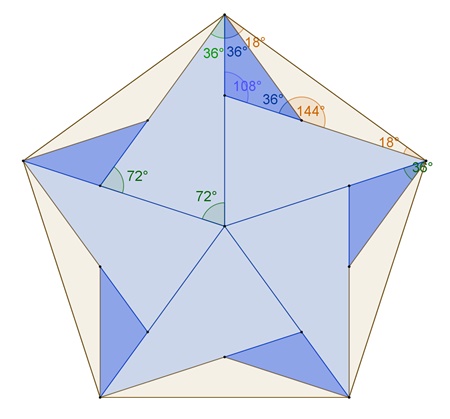
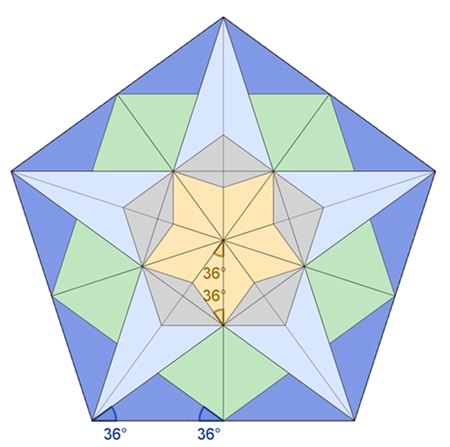
In diesem regelmäßigen Fünfeck befinden sich 5 kongruente dunkelblaue und 5
kongruente hellblaue goldene Dreiecke.
In diesem regelmäßigen Fünfeck befinden sich zwei weitere regelmäßige Fünfecke,
ein Pentagramm, goldene Dreiecke und viele goldene Schnitte.
|