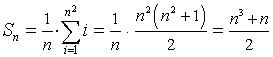Magische Quadrate

Festlegungen

Ein natürliches (normales) magisches Quadrat der Ordnung (Kantenlänge) n ist eine quadratische Anordnung der Zahlen 1,2,...,n², wobei die Summen jeder Zeile, jeder Spalte und jeder der beiden Diagonalen den gleichen Wert besitzen. Dieser Wert wird magische Summe genannt.

Ist die kleinste vorkommende Zahl größer oder gleich 1 so spricht man allgemein von einem magischen Quadrat, wenn jede Zahl nur einmal vorkommt.

Magische Quadrate der Ordnung n gelten als äquivalent, wenn sie durch Drehung oder Spiegelung ineinander übergeführt werden können.

Oft wird ein magisches Quadrat der Ordnung n als magisches n x n-Quadrat bezeichnet.

Eigenschaften

1) Durch Rotation um 90°, 180° und 270° um den Mittelpunkt des Quadrats sowie durch Spiegelung an den Hauptachsen und Diagonalen des Quadrats entsteht aus einem magischen Quadrat wieder ein magisches Quadrat. Diese acht magischen Quadrate sind äquivalent; es genügt, eines davon zu untersuchen.
Es hat sich eingebürgert, die Frénicle-Standardform zu verwenden:

Das Element in der linken oberen Ecke [1,1] ist das kleinste der vier Elemente in den Ecken.

Das Element rechts daneben [1,2] ist kleiner als das Element darunter [2,1].

2) Für die Zeilen-, Spalten- bzw. Diagonal-Summe (magische Zahl) eines natürlichen magischen Quadrats gilt:

Die Zeilen-, Spalten- bzw. Diagonal-Summe eines natürlichen magischen Quadrats von n = 3 bis n = 10 beträgt: 15, 34, 65, 111, 175, 260, 369 und 505.

3) Ein magisches Quadrat bleibt magisch, wenn man jede Zahl mit einer Konstanten C addiert, subtrahiert, multipliziert oder dividiert, z.B:

o steht an Stelle von + – * :

Anzahl verschiedener magischer Quadrate

Es gibt ein triviales magisches Quadrat mit Kantenlänge 1, jedoch keines mit Kantenlänge 2. In der Frénicle-Standardform oder einer anderen Grundform gibt es:

1                       magisches 3 x 3-Quadrat
880                   magische 4 x 4-Quadrate (1693 von Frénicle de Bessy gefunden)
275305224       magische 5 x 5-Quadrate (1973 von Richard Schroeppel berechnet)

1,78 ·10¹⁹magische 6 x 6-Quadrate (1998 von K. Pinn und C. Wieczerkowski abgeschätzt)

3,80 ·10³⁴ magische 7 x 7-Quadrate ( " , von W. Trump bestätigt)

Darüber hinaus ist die Anzahl magischer Quadrate bis zur Ordnung 10 näherungsweise bekannt.

Was macht die Beschäftigung mit normalen magischen Quadraten mit zunehmender Ordnung n so schwierig?

Die Wahrscheinlichkeiten (Ws) dafür, durch zufälliges Setzen der n² Zahlen von 1 bis n² ein normales magisches Quadrat der Ordnung n zu erhalten, nimmt mit zunehmendem n ab, wobei gilt: n! = 1· 2· 3 · ... · n.

n	Ws
3	8 : 9! 2,2·10^-5
4	7040 : 16! 3,4·10^-10
5	275305224 : 25! 1,8·10^-17
6	1,8 · 10¹⁹ : 36! 4,8·10^-23
7	3,8 ·10³⁴ : 49! 6,2·10^-29
usw.

Ohne bekannte Strukturen oder Bildungsgesetze für magische Quadrate wird es zunehmend aussichtslos rein zufällig ein magisches Quadrat zu erzeugen.

Variationen magischer Quadrate

Halbmagische (semimagische) Quadrate

Nur die Zeilensummen und Spaltensummen sind gleich groß.

Die magische Summe ist hier 34, die Diagonalsummen sind ungleich 34.

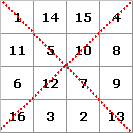
Pandiagonale magische (panmagische) Quadrate

Bei einem pandiagonalen magischen Quadrat muss nicht nur die Summe der Diagonalen, sondern auch die der gebrochenen Diagonalen gleich sein. Die gebrochenen Diagonalen verlaufen parallel zur Haupt- bzw. Nebendiagonale, wobei Elemente außerhalb des Quadrats um eine Kantenlänge verschoben werden.
Die magische Summe ist hier 65. Auch längs der gleichfarbig gestrichelten Linien ergibt sich als Summe 65. Bei den entsprechenden parallelen Linien zur Nebendiagonale ergibt sich als Summe ebenfalls 65.

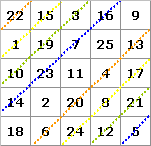
(Punkt)Symmetrische magische Quadrate

Erfüllt ein magisches Quadrat zusätzlich die Bedingung, dass die Summe zweier Zahlen in Zellen, die punktsymmetrisch zum Mittelpunkt des Quadrats liegen, gleich n² + 1 ist, so wird es (punkt)symmetrisches magisches Quadrat genannt.

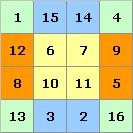
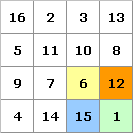
Beispiel für das magische 4x4-Quadrat:

6 + 11 = 17, 13 + 4 = 17, 15 + 2 = 17.
Es gibt insgesamt 384 (punkt)symmetrische magische 4x4-Quadrate.

In den jeweils gleich gefärbten, symmetrisch liegenden Zellen ergibt sich bei einem magischen 4x4-Quadrat ebenfalls die Summe 34.

Ultramagische Quadrate

Magische Quadrate, die sowohl symmetrisch als auch pandiagonal sind, nennt man ultramagisch.

Konzentrische magische Quadrate

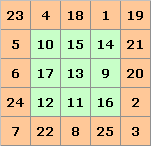
Ein konzentrisches oder umrandetes magisches Quadrat ist ein magisches Quadrat, das auch dann noch magisch bleibt, wenn man seinen Rand entfernt.
Die magische Summe ist hier 65. Das innere magische Quadrat hat die magische Summe 39.

Eingebettete magische Quadrate

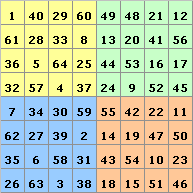
Ein eingebettetes magisches Quadrat ist ein Quadrat, in dem eine oder mehrere magische Quadrate eingebettet sind.
Die magische Summe ist hier 260. Die vier eingebetteten magischen Quadrate haben jeweils die magische Summe 130.

Selbstkomplementäre magische Quadrate

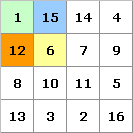
Wenn jede Zahl z eines natürlichen magischen Quadrats der Ordnung n durch sein Komplement n²+1-z ersetzt wird, entsteht ein neues magisches Quadrat. Wenn das neue magische Quadrat zum Ausgangsquadrat äquivalent ist, d.h. durch Drehungen und Spiegelungen auf dieses abgebildet werden kann, spricht man von einem selbstkomplementären magischen Quadrat. Manchmal wird es auch selbstähnlich genannt.
Die magische Summe ist hier 65. Das rechte magische Quadrat ist komplementär zum linken. Die beiden magischen Quadrate sind punktsymmetrisch zueinander.

Vollkommen perfekte magische Quadrate

Man spricht von einem vollkommen perfekten magischen Quadrat, wenn es folgende drei Eigenschaften besitzt:

1. Jedes beliebige 2x2-Teilquadrat besitzt immer die gleiche Summe S = 2 (n² + 1)

2. Die Summe von zwei Elementen einer Diagonalen, deren Abstand n/2 ist, besitzt immer den Wert ½ S = 2 (n² + 1)

3. Es handelt sich um ein Quadrat der Ordnung n = 4k, k = 1, 2, 3, ....

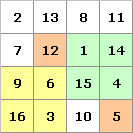
Die magische Summe ist hier 34.
Zu 1) Beispiele: 9+6+3+16=34, 1+14+4+15=34
Zu 2) 16+1=17, 6+11=17, 5+12=17, 15+2=17

Zusammengesetzte magische Quadrate

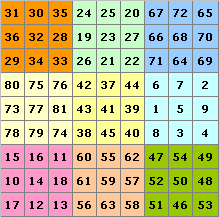
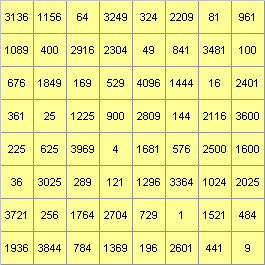
Zusammengesetzte magische Quadrate sind aus mehreren magischen Quadraten zusammengesetzt.
Die magische Summe ist hier 369.

Bimagische Quadrate

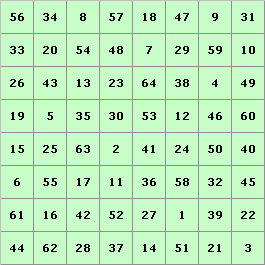
Ein magisches Quadrat heißt bimagisch, wenn es auch magisch bleibt, nachdem alle Zahlen quadriert worden sind.
Das folgende bimagische Quadrat hat G. Pfeffermann 1890 entdeckt.
Das linke magische Quadrat hat die magische Summe 360, das rechte dazu bimagische Quadrat die magische Summe 11180.

Primzahlenquadrate

Alle Zahlen des magisches Quadrats sind Primzahlen.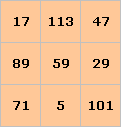

Geschichtliches

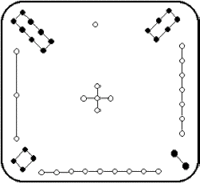
Das älteste bekannte magische Quadrat geht vermutlich auf den Kaiser Loh-Shu zurück, der ungefähr um 2800 v.Chr. in China gelebt hat. Die ungeraden Zahlen werden als weiße Punkte und die geraden Zahlen als schwarze Punkte dargestellt.
Durch die Farbzuordnung besitzt diese Darstellung auch eine philosophische und zahlenmystische Bedeutung.
Weiß ist die Farbe des Symbols Yang. Damit vertritt es die Eigenschaften des Symbols Yang. Die ungeraden Zahlen werden dem Männlichen zugeordnet.
Schwarz ist die Farbe des Symbols Yin. Die geraden Zahlen werden damit dem Weiblichen zugeordnet. (s. Zahlenmystik)

Als Detail in dem Kupferstich Melencolia I (1514) von Albrecht Dürer ist ein magisches 4 x 4-Quadrat zu finden.

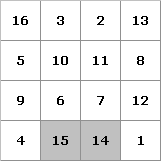
In der Mitte der unteren Zeile steht 1514, das Entstehungsjahr des Bildes und das Todesjahr der Mutter von Albrecht Dürer.

Hexen-Einmaleins in Goethes „Faust“

Mephisto spricht zu Faust in der Hexenküche:

"Du mußt verstehn!
Aus Eins mach' Zehn,
Und Zwei laß gehn,
Und Drei mach' gleich,
So bist Du reich.
Verlier' die Vier!
Aus Fünf und Sechs,
So sagt die Hex',
Mach' Sieben und Acht,
So ist's vollbracht:
Und Neun ist Eins,
Und Zehn ist keins.
Das ist das Hexen-Einmal-Eins!"

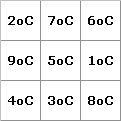
Mögliche Darstellung als semimagisches Quadrat:

Zunächst ist bei der Nummerierung die Feldnummer gemeint.

Feld 1 die Zahl 10, Feld 2 die Zahl 2, Feld 3 die Zahl3.

"So bist Du reich." Die Zeilensumme 15 ist nun bekannt.

Feld 4 die Zahl 0 ("verlieren"), Feld 5 und 6 die Zahlen 7 und 8.

"So ist's vollbracht:", die letzte Zeile mit den Zahlen 5, 6, 4 in den Feldern 7, 8, 9 ergibt sich logisch von selbst bei einem semimagischen Quadrat, da Spaltensumme = Zeilensumme = 15.

"Und Neun ist Eins" wird als ein semimagisches Quadrat interpretiert.

"Und Zehn ist keins" bedeutet, es gibt kein 10. Feld.

10	2	3
0	7	8
5	6	4

Internetquellen:

https://de.wikipedia.org/wiki/Magisches_Quadrat

http://www.hp-gramatke.de/magic_sq/index.htm

http://www.magic-squares.info

Zurück
Zurück zur Startseite