|
Tonhöhen und Intervalle in der Musik Intervalle in reiner Stimmung
Unter einem Intervall versteht man in der Musik den Tonhöhenabstand zweier
Töne.
Bereits Pythagoras (ca. 570 - 500 v. Chr.)
erkannte, dass wohltönende Intervalle ein ganzzahliges Verhältnis der
Saitenlänge eines schwingenden Saitenteils zur ganzen Saitenlänge
eines Monochords haben.
Ton
Saitenlängenverhältnis
Monochord
Frequenzverhältnis
Eine Seite, die den Ton c‘ erzeugt, schwingt 264-mal pro Sekunde, d.h. der
Ton c‘ hat damit eine Frequenz von 264 Hz (Hertz). Die Oktave c‘‘ hat dann
die Frequenz 528 Hz.
Bemerkung: Statt c‘, c'', ... wird auch c1,
c2,
... verwendet.
Intervalle bei der Tonleiter in C-Dur und c-Moll
Bei der reinen Stimmung stehen die Intervalle in ganzzahligen Verhältnissen. Frequenzen der C-Dur Tonleiter in reiner Stimmung mit Grundton c‘
NR: 9/8⸱264 = 297, 5/4⸱264 = 330, 4/3⸱264 = 352, 3/2⸱264 = 396, 5/3⸱264
= 440, 15/8⸱264 = 495
Als reine Stimmung wird ein musikalisches Tonsystem bezeichnet, bei
dem die Dur- und Molldreiklänge nur reine Quinten (mit dem
Frequenzverhältnis 3/2) und reine Terzen (mit den
Frequenzverhältnissen 5/4 und 6/5) enthalten.
Die quintenreine (pythagoräische) Stimmung ist dadurch
gekennzeichnet, dass die Stimmung durch reine Quinten gegeben ist. Dies ist
z.B. bei Streichinstrumenten der Fall.
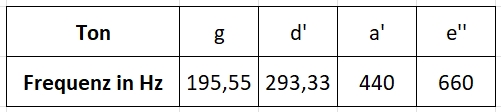
Die Geige wird normalerweise auf den Kammerton a‘ = 440 Hz gestimmt. Dann
hat das darüberliegende e‘‘ = 660 Hz (Frequenzverhältnis 3/2), das
darunterliegende Geigen-d‘ = 293,33.. Hz und das tiefe Geigen-g = 195,55..
Hz.
Bei der C-Dur Tonleiter gilt: e‘‘/a‘ = 660/440 = 1,5, a‘/d‘ = 440/297
≈ 1,48, d‘/g =
297/198 = 1,5
Bei der Violine ist das Frequenzverhältnis zum jeweils vorhergehenden Ton 3
: 2.
NR: e‘‘/a‘ = 660/440 = 1,5, a‘/d‘ = 440/293,333...
=
1,5, d‘/g = 293,33.../195,555... = 1,5
Hier zeigt sich ein Widerspruch bei reiner Stimmung vom Grundton c‘ bzw. vom
Grundton g ausgehend. Die reine Stimmung kann nicht für alle Tonarten
gelten. Intervalle in mitteltöniger Stimmung
Von ca.
1550 bis 1750 waren bei Tasteninstrumenten mitteltönige Stimmungen üblich.
Ihr Charakteristikum sind acht etwa gleich gut und vier schlecht klingende
Moll- bzw. Durtonarten. Eine der schlecht klingenden Tonarten beinhaltet
eine sehr stark verstimmte Quinte, die sogenannte Wolfsquinte.
Die 1/4-Komma-mitteltönigen Stimmung ist eine verbreitete Form der
mitteltönigen Stimmung. Die wichtigsten Intervalle, wie Quinten, sind
relativ rein gestimmt, acht große Terzen in den wohlklingenden Tonarten sind
auch rein. Der Ganzton entspricht bei dieser Stimmung dem Mittel von großem
und kleinem Ganzton der reinen Stimmung (daher der Name). Intervalle in wohltemperierter und gleichstufiger Stimmung
Als wohltemperierte Stimmung bezeichnet man ein temperiertes
Stimmungssystem für Musikinstrumente mit festgelegten Tonhöhen, z.B bei
Klavier und Orgel, welche die Verwendung aller Tonarten ermöglicht im
Unterschied zur reinen Stimmung.

Erstmals belegt ist diese Stimmung für die 1668–1673 von Christian Förner
(1609 – 1678) erbaute Förner-Orgel. Andreas Werckmeister (1645 –
1706) veröffentlichte 1681 die erste Beschreibung verschiedenen Stimmungen,
auch der wohltemperierten Stimmung.
Die Tonfrequenz wird bei einem Halbtonschritt um den Faktor 1,059463 erhöht.
Nach 12 Halbtonschritten ergibt sich die zugehörige Oktave:
In der Musiktheorie gibt es den Begriff Cent.
100 Cent ist das Frequenzverhältnis eines gleichstufigen Halbtons.
Es gilt: 1 Cent =
2 1/1200 ≈ 1,000577789,
100 Cent = 2
100/1200
= 2 1/12 ≈ 1,059463,
1200 Cent = 2 1200/1200
= 2, 0 Cent = 2
0/1200 = 20 = 1.
Die 12 Töne von c‘ bis c‘‘ in gleichstufiger Stimmung mit a‘ = 440 Hz
Bei der gleichstufigen Stimmung bleibt die Oktavenreinheit erhalten, während
alle anderen Intervalle geringfügig verändert werden.
Die C-Dur Tonleiter in Hz und Cent
Die Frequenzverhältnisse in Cent werden addiert, während die zugehörigen
einfachen Frequenzverhältnisse multipliziert werden.
Cent1 + Cent2 = 2 (Cent1 + Cent2)/1200 = 2 Cent1/1200
⸱ 2 Cent2/1200 (1.
Potenzgesetz)
Beispiel: 200 + 500 = 700 oder 1,122⸱1,335 = 1,498 (3 D)
Eine gleichstufige Stimmung berechnete 1584 als erster der Chinese
Chu-Tsai-yü (1536 – 1610). Der italienische Kapellmeister Gioseffo
Zarlino (1517 – 1590) entwickelte 1588 eine geometrische Darstellung der
gleichstufigen Stimmung.
Der Quintenzirkel
Auf dem äußeren Kreis stehen die Dur-Tonarten, im inneren Kreis die
Moll-Tonarten mit der gleichen Anzahl an Vorzeichen. Die Paralleltonarten
sind jeweils eine kleine Terz tiefer.
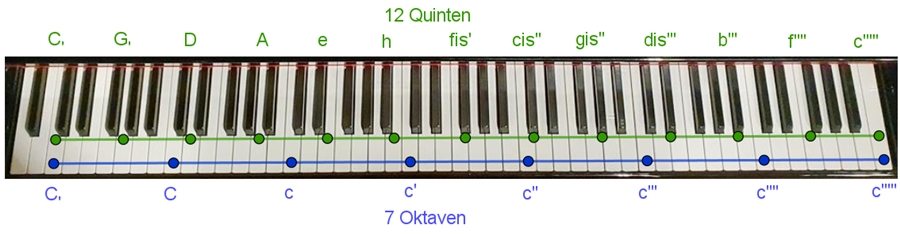
Nach 12 aufeinander folgende Quinten von C-Dur ausgehend entsteht ein
7 Oktaven höheres C-Dur. An der Klaviertastatur kann dies schön veranschaulicht werden.
Das pythagoräische Komma
12 aufeinanderfolgende Quinten und 7 aufeinanderfolgende Oktaven müssten vom
gleichen Grundton ausgehend wieder den gleichen Ton ergeben.
Dies ist nicht der Fall, wie folgende Rechnung zeigt: 1,5 12 ≈ 129,746; 27 = 128
Die Differenz 129,746 – 128
≈ 1,746 heißt
pythagoräisches Komma.
Dies ist der Grund, weshalb Tasteninstrumente mit 12 Halbtönen pro Oktave
nicht in allen Tonarten in reinen Intervallen gespielt werden können.
Deshalb wurde die wohltemperierte und gleichstufige Stimmung
entwickelt.
Durch die gleichstufige Stimmung wird das Pythagoräische Komma, das
zwischen der 12. Quinte und der 7. Oktave über einem Ton besteht,
ausgeglichen.
Zurück Zurück zur Startseite |
 1
1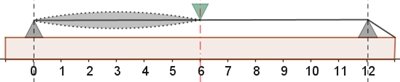 2 : 1
2 : 1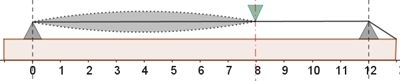 3 : 2
3 : 2 4 : 3
4 : 3 5 : 4
5 : 4