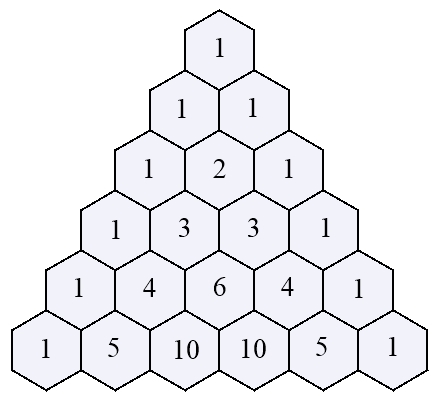
Pascalsches Dreieck
Zeilen-
Pascalsches Zeilensumme: nummer:
Dreieck
0
1
1
= 20
1
1 1
2
= 21
2
1 2 1
4
= 22
3
1 3
3 1
8
= 23
4
1
4 6
4
1 16 =
24
5
1
5
10
10 5 1
32 = 25 ...
| | | | | |
0-
1-
2- 3-
4-
5-te
Spalte in Zeile 5 Zeilen-
Pascalsches Binomische Formeln: nummer:
Dreieck
0
1
(a+b)0
= 1
1
1 1
(a+b)1
= a+b
2
1 2 1
(a+b)2
= a2+2ab+b2
3
1 3
3 1
(a+b)3 = a3+3a2b+3ab2+b3
4
1 4
6 4
1
(a+b)4 = a4+4a3b+6a2b2+4ab3+b4
5
1 5
10 10
5 1
(a+b)5 =
1a5+5a4b+10a3b2+10a2b3+5ab4+1b5
...
Allgemein
gilt:
Formeln: n = Zeilennummer, k = Spaltennummer
Beispiel:
6
+ 4
=
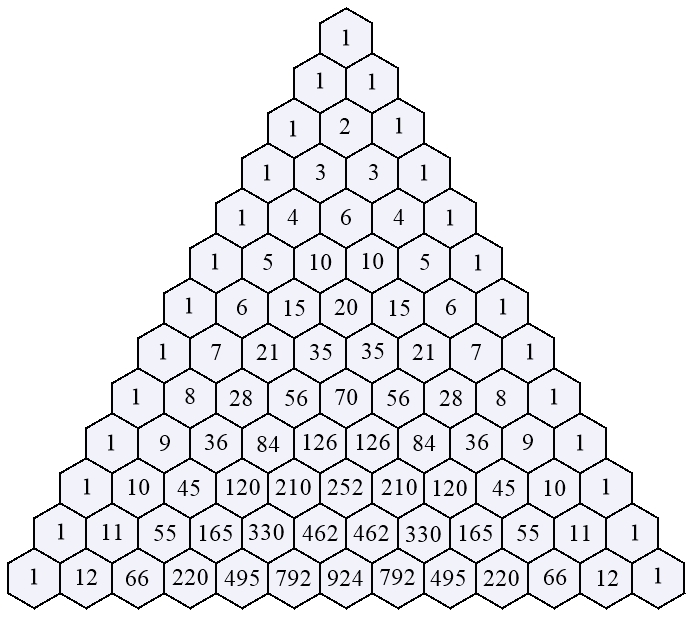
10 Symmetrisches Pascalsches Dreieck bis zur Reihe 12: Zeilennr:
0
1 1 1 1 2 1 2 1 3 1 3 3 1 4 1 4 6 4 1 5 1 5 10 10 5 1 6 1 6 15 20 15 6 1 7 1 7 21 35 35 21 7 1 8 1 8 28 56 70 56 28 8 1 9 1 9 36 84 126 126 84 36 9 1 10 1 10 45 120 210 252 210 120 45 10 1 11 1 11 55 165 330 462 462 330 165 55 11 1 12 1 12 66 220 495 792 924 792 495 220 66 12 1 Asymmetrisches Pascalsches Dreieck bis zur Reihe 12:
Zeilennr:
0 1
1 1 1
2 1 2 1
3 1 3 3 1
4 1 4 6 4
1
5 1 5 10 10 5
1
6 1 6 15 20 15
6 1
7 1 7 21 35 35
21 7 1
8 1 8 28 56 70
56 28 8 1
9 1 9 36 84 126 126
84 36 9 1
10 1 10 45 120 210 252 210 120
45 10 1
11 1 11 55 165 330 462 462 330 165
55 11 1
12 1 12 66 220 495 792 924 792 495 220
66 12 1
Weitere
Eigenschaften:
Alle Zahlen in
einer Zeile mit einer Primzahl als Zeilennummer sind durch diese teilbar. In der 1. Spalte des
asymmetrischen Dreiecks bzw entsprechenden Diagonalen im symmetrischen Dreieck
stehen die natürlichen Zahlen . In der n-ten Zeile steht die Zahl
In der 2. Spalte des
asymmetrischen Dreiecks bzw entsprechenden Diagonalen im symmetrischen Dreieck
stehen die Dreieckszahlen . In der n-ten Zeile steht die Zahl
In der 3. Spalte und n-ten Zeile
des asymmetrischen Dreiecks bzw entsprechenden Diagonalen im symmetrischen
Dreieck steht die Zahl
usw.
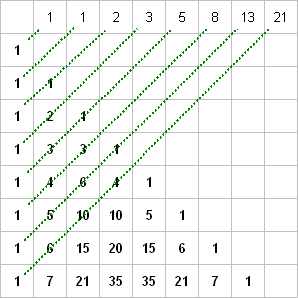
Bei entsprechend schräger Diagonalbildung ergeben sich als Summenglieder die Fibonacci-Zahlenfolge: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ... ( s.
Fibonacci-Zahlen )
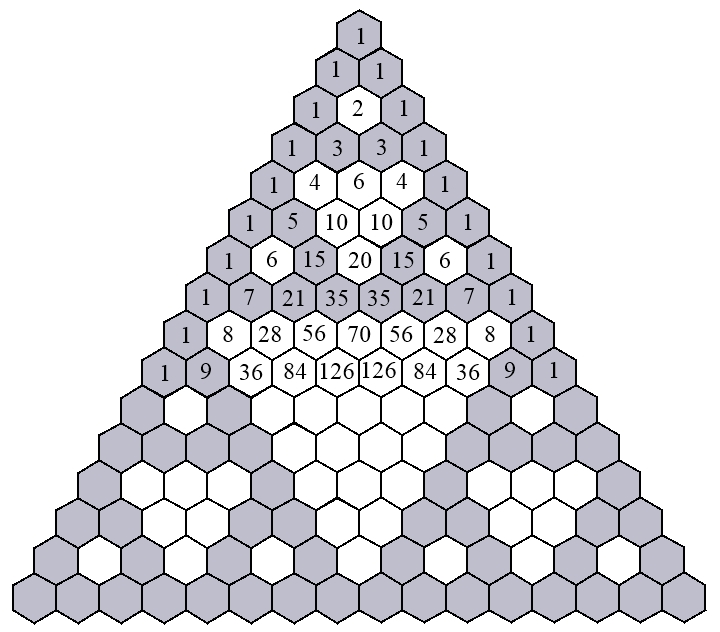
Pascalsches Dreieck als Sierpinski-Dreieck, bis zur Reihe 16 - bis zur Reihe 64:
dunkles Sechseck
= ungerade Zahl,
helles Sechseck
= gerade Zahl
Weihnachtsbaum als Pascaldreieck
Zurück Zurück zur Startseite |