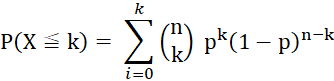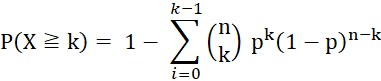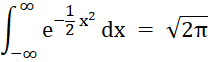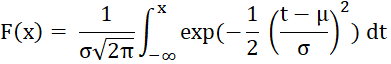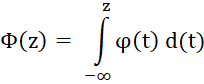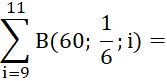|
Binomial- und Normalverteilung
Kombinatorik zur Binomialverteilung n-Tupel:
Ein n-Tupel ist eine
Zusammenfassung von n Objekten x1, x2, x3,
…, xn in einer Liste. Die Objekte müssen nicht verschieden sein.
Tupel werden meist mit runden Klammern und Kommas (Strichpunkten) notiert
(x1, x2, x3, …, xn)
Anzahl der n-Tupel bei n
verschiedenen Objekten:
Anzahl der Möglichkeiten für die 1. Stelle:
n
..
Anzahl der Möglichkeiten für die n. Stelle:
1
Nach dem Zählprinzip gibt es
insgesamt n٠(n – 1)٠(n
– 2)٠ …
٠3٠2٠1
Als Abkürzung schreibt man
Beispiel:
3! = 6 mögliche 3-Tupel mit den Buchstaben a, b und c:
abc, acb, bac, bca, cab, cba
Permutation:
Die verschiedenen Reihenfolgen von n Objekten
im n-Tupel heißt Permutation,
Permutation mit Wiederholung mit nur 2 verschiedenen Zahlen, 0 und 1.
Wie viele verschiedene Reihenfolgen gibt es für ein n-Tupel mit k-mal 1 und
(n-k)-mal 0?
Ein 5-Tupel mit 2-mal 1 und 3-mal 0
liefert 10 mögliche Reihenfolgen:
Allgemein ergibt sich bei einem n-Tupel mit k-mal 1 und (n – k)-mal 0
bzw. k-mal 0 und (n – k)-mal 1
Die Binomialverteilung
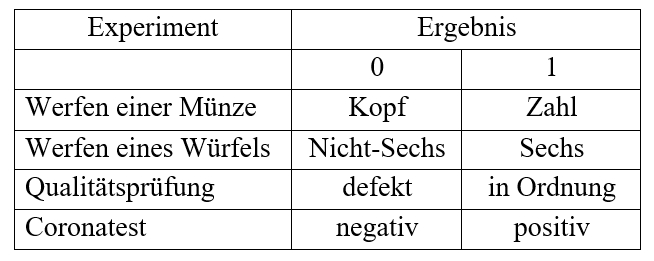
Bernoulli-Experiment:
Ein Zufallsexperiment mit der Ergebnismenge Ω
= {0, 1}, den Wahrscheinlichkeiten P({1}) = p und P({0}) = 1 – p, heißt
Bernoulli-Experiment mit der
Trefferwahrscheinlichkeit p.
Beispiele:
Bernoulli-Kette:
Ein n-stufiges Zufallsexperiment
heißt Bernoulli-Kette der Länge n
mit dem Parameter p, wenn gilt:
Menge aller 3-Tupel:
{(0,0,0), (1,0,0), (0,1,0), (0,0,1), (1,1,0), (0,1,1), (1,0,1), (1,1,1)}
Für eine Bernoulli-Kette der Länge n gilt:
P(„genau k Treffer“) =
Die Wahrscheinlichkeitsverteilung
heißt Binomialverteilung B(n; p) mit den Parametern n und p.
Die Zufallsvariable (Zufallsgröße) X mit P(X = k) = B(n; p; k) heißt
binomial verteilt nach der
Binomialverteilung B(n; p).
Erwartungswert μ
von X: μ = n
p
Varianz von X:
Var(X) = n p (1 – p)
Standardabweichung σ von X:
σ(X) =
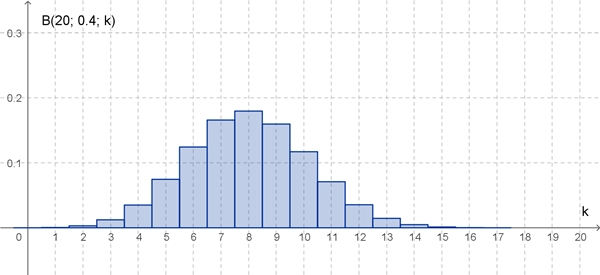
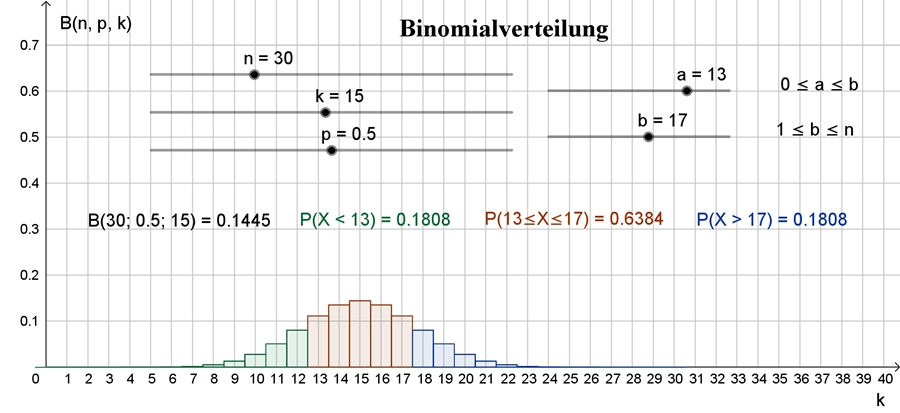
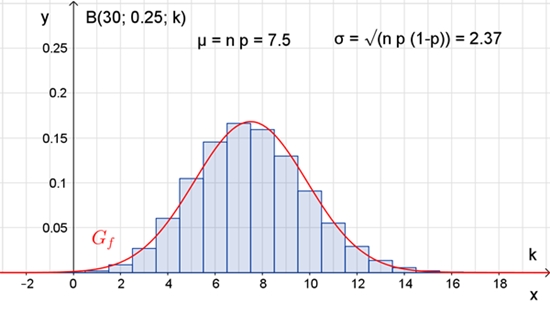
Graphische Veranschaulichung
der Binomialverteilung als Histogramm bei einer Bernoulli-Kette der Länge n
= 20 und der
Trefferwahrscheinlichkeit p = 0,4.
Erwartungswert μ = 20٠0,4 = 8,
Standardabweichung
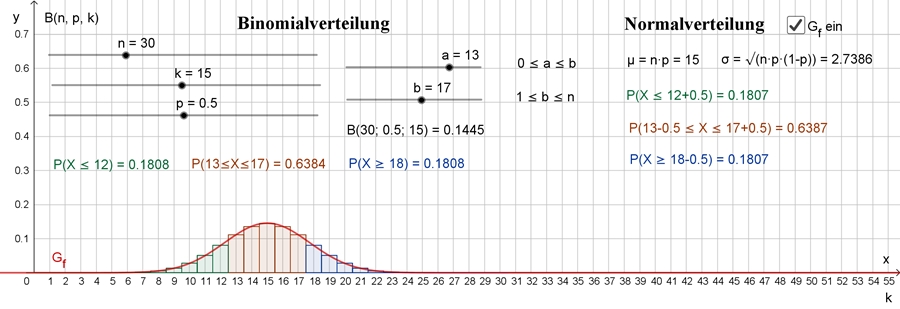
Berechnung von Wahrscheinlichkeiten (Ws) mit der Binomialverteilung
n = Anzahl der Wiederholungen des Zufallsexperiments mit den Ergebnissen 0
(Niete) oder 1 (Treffer), der Trefferwahrscheinlichkeit p und der
Zufallsvariablen X.
Ws für genau k Treffer:
Ws für höchstens k Treffer:
Ws für mindestens k Treffer:
Graphische Darstellung der
Binomialverteilung mit Animation
Berechnung von Ws bis n = 2000
Die Glockenkurve mit der
Gleichung f(x)
= e–1/2
x²,
x ϵ ℝ
Für die Glockenkurve
gilt (Euler-Poisson- oder Gauß-Integral):
Der
Flächeninhalt zwischen Funktionsgraphen Gf und x-Achse ist gleich
der Wurzel aus 2 π.
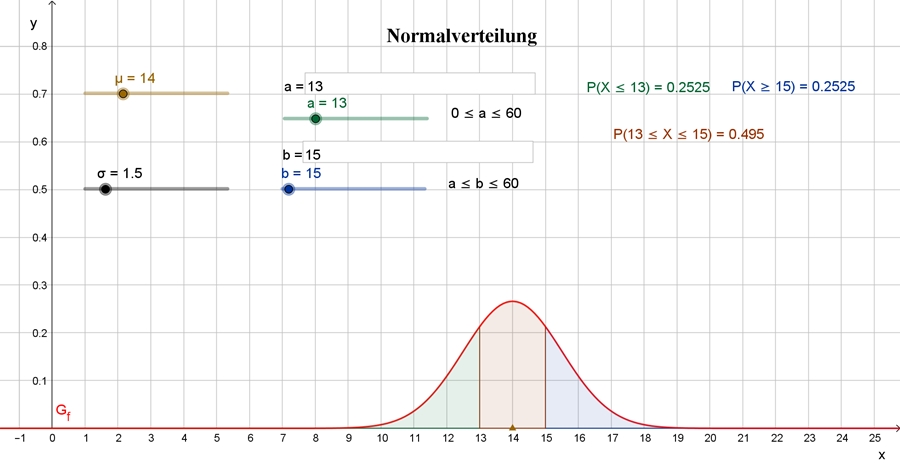
Normalverteilung:
Eine stetige Zufallsvariable (Zufallsgröße)
X hat eine Gauß- oder
Normalverteilung mit dem Erwartungswert μ (-∞ < μ < ∞) und der Varianz
σ² (σ² > 0) bzw. der Standardabweichung σ, wenn X die folgende
Wahrscheinlichkeitsdichte hat
für x ϵ ℝ und exp( ) = e(
):
Die Verteilungsfunktion der
Normalverteilung ist gegeben durch
Es gilt:
F(∞) = 1, d.h. die
Summe aller Wahrscheinlichkeiten ist 1.
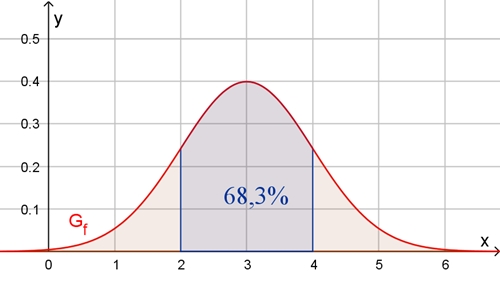
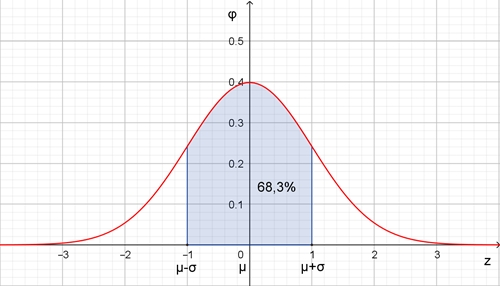
F(μ + σ) – F(μ – σ) ≈
0,683 = 68,3%
Im Intervall [μ – σ, μ + σ]
liegen 68,3% Zufallsvariablen
Im Intervall [μ–2σ, μ+2σ] liegen
95,4% Zufallsvariablen
Im Intervall [μ–3σ, μ+3σ] liegen
99,7% Zufallsvariablen
Graph
der Normalverteilung für
μ = 3, σ = 1
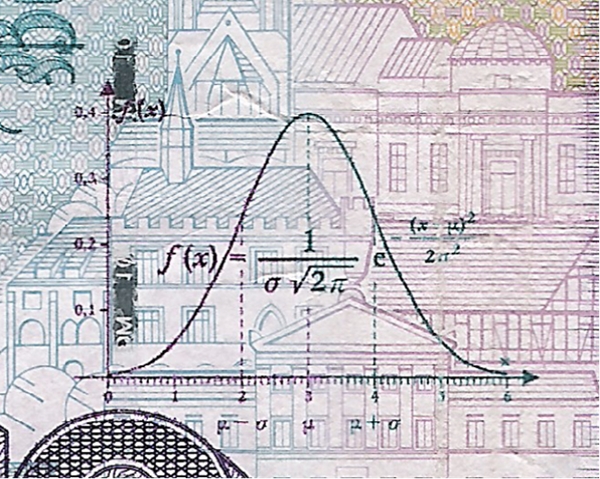
Die Normalverteilung als bedeutende Leistung von Carl Friedrich Gauß (1777 – 1855) auf dem alten Zehnmarkschein dargestellt, mit
Ausschnittvergrößerung:
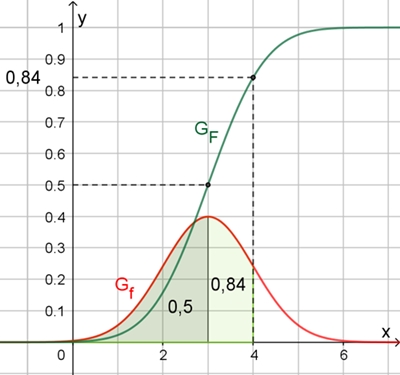
Graphen der Normalverteilung und Verteilungsfunktion für
für μ = 3,
σ = 1.
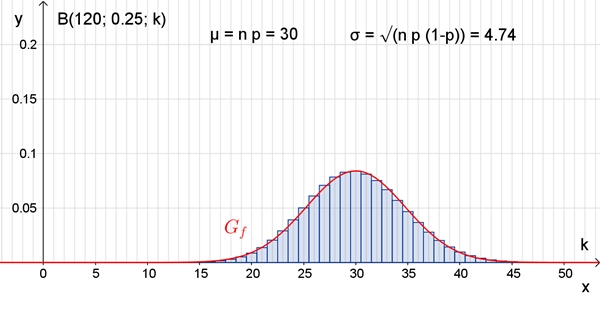
Zusammenhang zwischen Binomial- und Normalverteilung
Nach dem Satz von Moivre-Laplace konvergiert
die Binomialverteilung für n → ∞ gegen die Normalverteilung. Bei großem
Stichprobenumfang n kann die Binomialverteilung in sehr guter Näherung durch
die Normalverteilung ersetzt werden.
Graphen der Binomial- und Normalverteilung für n = 30 und n = 120, p = 0,25:
Graphische Darstellung der
Binomial- und Normalverteilung mit Animation
Von
Standardisierung spricht man,
wenn eine Zufallsvariable X so transformiert (umgewandelt) wird, dass die
resultierende Variable Z den Erwartungswert E(Z) = 0 und die Varianz Var(Z)
= 1 bzw. die Standardabweichung
σ(Z) = 1 hat. Die
Normalverteilung mit dem Erwartungswert bzw. Mittelwert μ = 0 und der
Standardabweichung σ = 1 wird
Standardnormalverteilung genannt.
Normalverteilung:
Standardisierte
Normalverteilung
mit
Standardisierte Verteilungsfunktion der Normalverteilung:
Graph der
Standardnormalverteilung
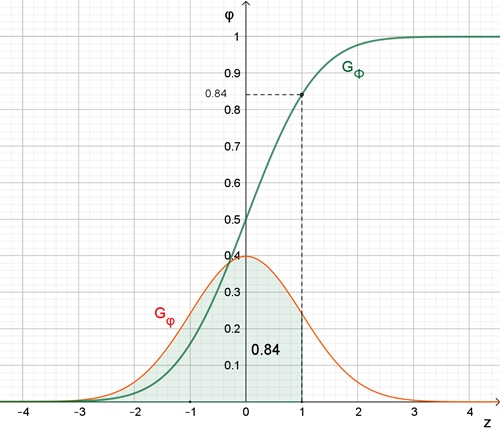
Die Graphen Gφ
und GΦ
der
standardisierten
Normalverteilung und Verteilungsfunktion
Für große n und 0 < p < 1
gilt:
Bemerkungen: Für die
standardisierte Normalverteilung und Verteilungsfunktion gibt es Tabellen,
mit deren Hilfe beliebige Normalverteilungen durch Z-Transformation
berechnet werden können.
Die Addition von 0,5 heißt
Stetigkeitskorrektur
Wegen der Achsensymmetrie von
Gφ gilt:
φ(-z) = φ(z).
Damit kann man sich in der Tabelle auf nur positive Werte von z beschränken.
1. Beispiel:
Verteilung der Größe von Männern in Deutschland mit 19 Jahren geboren 2000
Wie viele Männer sind höchstens 190 cm groß? P(X
≦ 190 cm) ≈ Φ(z)
Etwa 90,5% der Männer sind kleiner oder gleich 190 cm.
Wie viele Männer sind mindestens 165 cm groß?
P(X ≧ 165 cm) = 1 – P(X < 165) = 1 – P(X ≦ 164)
Etwa 97,4% der Männer sind größer oder gleich 165 cm.
2. Beispiel:
Wie groß ist die
Wahrscheinlichkeit, dass bei 60 Würfen mit einem Laplace-Würfel (alle
Augenzahlen sind gleichwahrscheinlich) mindestens 9- und höchstens 11-mal
die Sechs gewürfelt wird?
n = 60, p = 1/6,
μ
= n٠p
= 10,
σ
= √(n٠p٠(1–p)) = 5/√3 ≈ 2,8868
P(9 ≦ X ≦ 11) = P(X ≦ 11) – P(X ≦ 8)
≈
Die
Wahrscheinlichkeit dafür ist etwa 39,7%.
Exakte Berechnung mit der
Binomialverteilung: P(9 ≦ X
≦ 11) =
Der
Fehler durch die Näherung mit der Normalverteilung beträgt nur 0,1%. Mit
Hilfe des Computers lassen sich heute Wahrscheinlichkeiten bei der Binomial-
und Normalverteilung auch für große n direkt berechnen. |