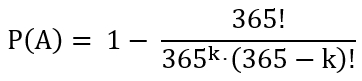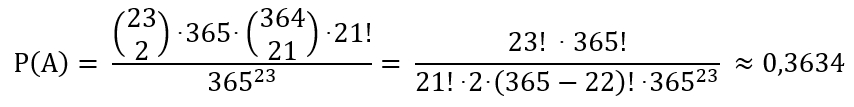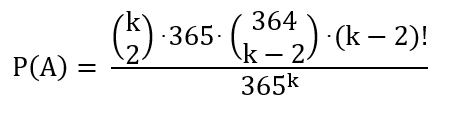Das Geburtstagsparadoxon

1. Fall:

In einem Zimmer befinden sich z.B. 23 Personen. Wie groß ist dann die Wahrscheinlichkeit, dass mindestens 2 Personen am gleichen Tag Geburtstag haben (Ereignis A)?
Es wird vorausgesetzt, dass die Geburtstage im Jahr mit 365 Tagen (kein Schaltjahr) gleich verteilt sind und sich keine Zwillingspaare (Drillingspaare usw.) darunter befinden.

Um diese Wahrscheinlichkeit P(A) zu berechnen geht man zunächst von der Gegenwahrscheinlichkeit (Wahrscheinlichkeit des Gegenereignisses) aus:
Wie groß ist die Wahrscheinlichkeit, dass keine 2 von 23 Personen am gleichen Tag Geburtstag haben, d.h. dass alle 23 Personen an verschiedenen Tagen Geburtstag haben?

Die (Laplace-)Wahrscheinlichkeit P(A) eines Ereignisses A erhält man, indem man die Anzahl |A| der für A günstigen Ergebnisse durch die Gesamtzahl m der möglichen Ergebnisse dividiert.

Entsprechendes gilt für das Gegenereignis , wobei gilt: 

Bei 2 Personen gilt: 

Bei 3 Personen gilt: 

. . .

Bei 23 Personen gilt: 

Damit gilt für die Wahrscheinlichkeit P(A):

Mit einer Wahrscheinlichkeit von ungefähr 50,7 % haben mindestens 2 von 23 Personen am gleichen Tag Geburtstag.

Das Ergebnis ist für viele Menschen verblüffend und wird deshalb als Paradoxon bezeichnet.

Allgemein gilt für die Wahrscheinlichkeit, dass mindestens 2 von k Personen am gleichen Tag Geburtstag haben:

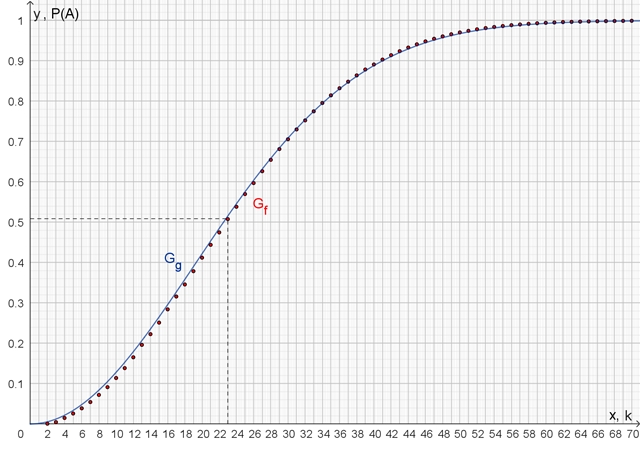
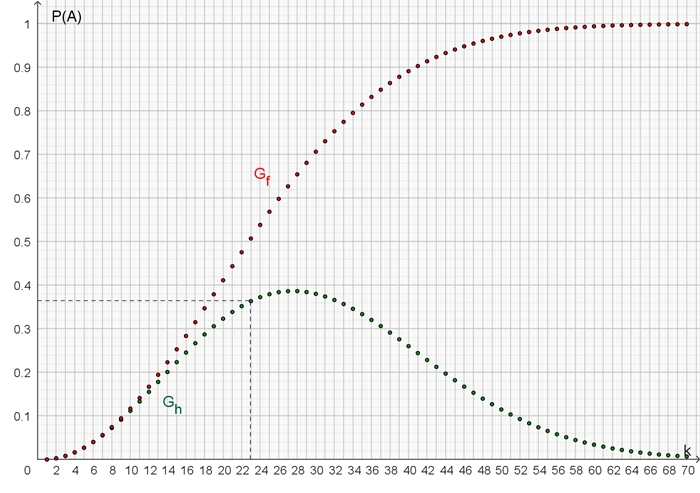
Grafische Darstellung G_f für die Wahrscheinlichkeit, dass mindestens 2 von k Personen am gleichen Tag Geburtstag haben

Näherung durch die Funktion mit der Gleichung 

2. Fall:

In einem Zimmer befinden sich z.B. 23 Personen. Wie groß ist dann die Wahrscheinlichkeit, dass genau 2 Personen am gleichen Tag Geburtstag haben (Ereignis A)?

Mit einer Wahrscheinlichkeit von ungefähr 36,3 % haben genau 2 von 23 Personen am gleichen Tag Geburtstag.

Allgemein gilt für die Wahrscheinlichkeit, dass genau 2 von k Personen am gleichen Tag Geburtstag haben:

Ab der Anzahl k = 28 von Personen wird wird es unwahrscheinlicher, dass genau 2 Personen (und nicht mehr Personen) am gleichen Tag Geburtstag haben.

Grafische Darstellung G_h für die Wahrscheinlichkeit, dass genau 2 von k Personen am gleichen Tag Geburtstag haben im Vergleich mit G_f

Zurück
Zurück zur Startseite