|
Fibonacci-Zahlen, goldener Schnitt und Natur
Fibonacci-Folge: 1,
1, 2, 3, 5, 8 ,13, 21, 34, 55, 89, 144, 233, ...
Die Formel für die Fibonacci-Folge lautet: Fn+2 = Fn+1 + Fn mit F1 = 1 und F2 = 1
Die
Quotienten zweier aufeinanderfolgender Fibonacci-Zahlen:
Die Quotienten zweier aufeinanderfolgender
Fibonacci-Zahlen nähern sich immer mehr der goldenen
Schnittzahl σ ≈ 0,61803 an. Die Kehrwerte
nähern sich der goldenen Schnittzahl τ ≈ 1,61803
Bei 5/8 beträgt die Abweichung von σ ungefähr
1%, bei 8/13 ungefähr 0,4% und bei 13/21 nur ungefähr 0,2%, ein Unterschied,
der in Zeichnungen schon nicht mehr erkennbar ist.
Die Fibonacci-Zahlen spielen
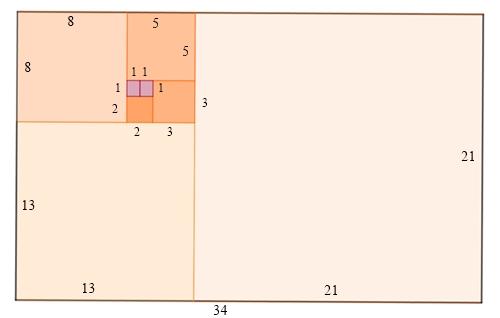
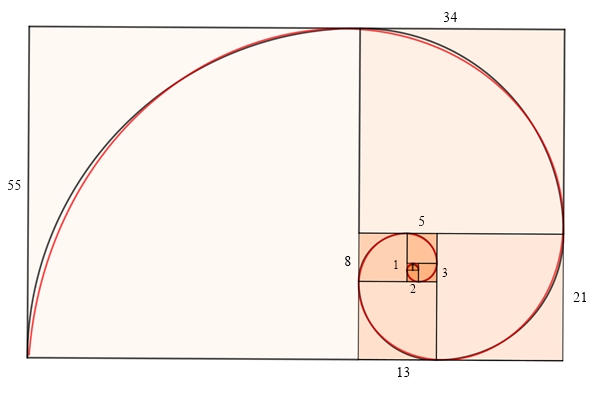
damit in Verbindung mit dem goldenen Schnitt eine bedeutende Rolle. Ineinander geschachtelte Quadrate, mit Fibonacci-Zahlen als Seitenlängen, die ein goldenes Rechteck immer besser annähern:
Die Summenformel
F1
+ F2
+ F3
+ … + Fn
= Fn+2
– 1
Begründung:
Fn+2
= Fn
+ Fn+1
oder Fn
= – Fn+1 + Fn+2
F1
= – F2 + F3
Addition:
F1
+ F2
+ F3
+ … + Fn = – F2
+ F3
– F3
+ F4
– F4
+ F3
–
…
– Fn+1
+ Fn+2
Größter
gemeinsamer Teiler von
Fn
und
Fn+1
ist 1, ggt(Fn, Fn+1) = 1
Begründung mit
Hilfe der vollständigen Induktion:
Induktionsanfang:
ggT( F1, F2) = 1
Die
Fibonacci-Zahlen spielen eine Bedeutung in der Natur
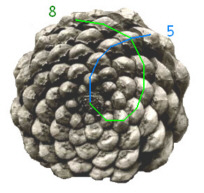
Der Pinienzapfen
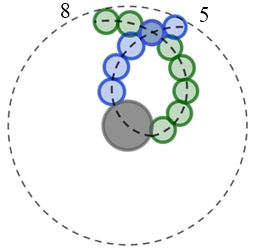
Die Anzahl der Samenschuppen von Pinienzapfen auf linksdrehenden und
rechtsdrehenden Spiralbahnen, die das Wachstum kennzeichnen, sind
aufeinanderfolgende Fibonacci-Zahlen, hier 8 und 5. Die spiralförmige Anordnung der Sonnenblumenkerne führt zu Fibonacci-Zahlen.
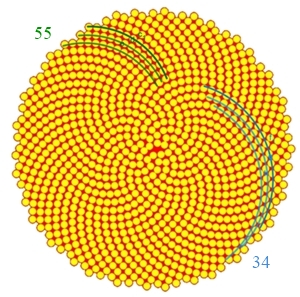
Die Anzahl der linksdrehenden Bögen von Samenkapseln im Vergleich zu den
rechtsdrehenden Bögen steht hier wie in den meisten Fällen im Verhältnis 55
zu 34. Es kann aber auch das umgekehrte Verhältnis sein.
Die spiralförmige Anordnung findet man bei den Samenständen vieler Pflanzen
und hängt mit dem
goldenen Winkel von 137,5° der Samenanordnung zusammen.
Spirale aus schwarzen Viertelkreisen in ineinander geschachtelten Quadraten
mit Fibonacci-Zahlen als Seitenlängen
Die rote Kurve ist die goldene Spirale, eine spezielle
logarithmische Spirale in Polarkoordinaten:
r(φ) = exp(k٠φ) mit
k = 4٠ln(τ) / (2π) ≈ 0,3064
und τ ≈ 1,61803 (goldene
Schnittzahl)
Spiralförmige Anordnungen findet man auch bei
Wirbelstürmen, Galaxien, Schneckengehäusen, Gehäusen von Ammoniten,
Fibonacci-Zahlen als Anzahl von Blütenblättern bei
einer Reihe von Blumen.
Die Haselwurtz hat 3 Blütenblätter.
Die Clematis hat 8 Blütenblätter.
Die Arnika hat 13 Blütenblätter.
Diese Margerite hat 21 Blütenblätter, es gibt aber auch Margeriten mit 34
Blütenblättern.
Dieses Gänseblümchen hat 34 Blütenblätter, es
gibt aber auch Gänseblümchen mit 21, 55 oder 89 Blütenblättern.
Diese Gerbera hat 55 äußere Blütenblätter.
Dieser Löwenzahn hat 144 Blütenblätter.
Die Anzahl der Blütenblätter hat in den
Fibonacci-Zahlen den wahrscheinlichsten Wert, mit statistischen
Abweichungen.
Die Fibonacci-Zahlen spielen in der Natur
eine besondere Rolle. Zurück Zurück zur Startseite |