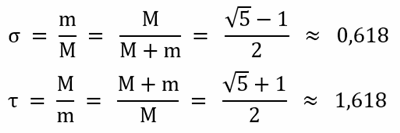Goldener Schnitt in Architektur und Kunst

Es gelten folgende Bezeichnungen und Beziehungen:

An Stelle von τ (tau) wird auch Φ (Phi) verwendet.

Vorbemerkung zum goldenen Schnitt in der Architektur und Kunst:

Der goldene Schnitt kommt als Verhältnis in vielfältiger Weise in der Natur und auch beim Menschen vor. Deshalb ist es naheliegend, dass der Mensch diese Proportion als angenehm oder schön empfindet.

Baumeister und Maler haben den goldenen Schnitt oder eine seiner Näherungen mit Hilfe der Fibonacci-Zahlen seit dem Altertum als Stilmittel wahrscheinlich meist intuitiv eingesetzt.

Die Quotienten zweier aufeinanderfolgender Fibonacci-Zahlen in der

Fibonacci-Folge 1, 1, 2, 3, 5, 8 ,13, 21, . . .

liefern eine zunehmend bessere Näherung des goldenen Schnitts,

z.B.  3/5 = 0,6,  5/8 = 0,625,  8/13 ≈ 0,615,  13/21 ≈ 0,619

Bei vielen Bauwerken und Gemälden wurde der goldene Schnitt nicht dokumentiert und kann nur nachträglich durch Bildanalyse spekulativ zugeordnet werden. Eine einfache Näherung ist 5/8  = 0,625 und stimmt auf 1% mit dem genauen Wert von σ überein.

Der berühmte Architekt Le Corbusier (1887 – 1965) hat den goldenen Schnitt bewusst häufig als Stilmerkmal in seinen Bauwerken verwendet.

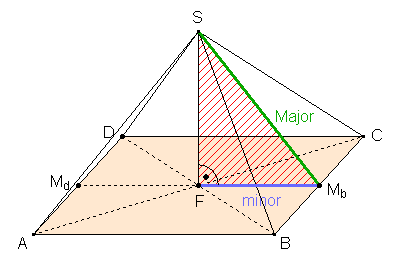
a) Beispiele in der Architektur

Die Cheops-Pyramide (2470 v. Chr.)

Die Cheops-Pyramide, die um 2590 bis 2470 vor Christus bei Gizeh in Ägypten erbaut wurde,  hat einen quadratischen Grundriss, wobei die Seitenlänge des Quadrats ursprünglich 230,4 m und die Höhe der Pyramide ursprünglich 146,6 m war.

Zufall oder angewandtes Wissen?

Das Dreieck FM_bS wird Keplerdreieck genannt (s. Konstruktionen)

Der Parthenon (438  v. Chr.) in Athen und die Walhalla bei Regensburg (1842)

Der größte Tempel auf der Akropolis wurde während der Regierungszeit von Perikles unter der Leitung des Baumeisters Phidias  von  447 - 438  v. Chr. erbaut.

Das große rot umrandete Rechteck  ist ein goldenes Rechteck.

Die Walhalla wurde unter König Ludwig I. von Leo von Klenze in den Jahren 1830 bis 1842 nach dem Vorbild des Parthenon in Athen gebaut. Sie liegt auf einer Anhöhe linkerseits der Donau bei Donauwörth, 10 km von Regensburg entfernt.

Die romanische Fassade der Kirche Sainte-Trinité  in Caen

Die Kirche Sainte-Trinité war zunächst Klosterkirche. Baubeginn war 1060; 1125 wurde das Tonnengewölbe durch ein Rippengewölbe ersetzt.

Romanisches Portal der Schottenkirche in Regensburg (1180)

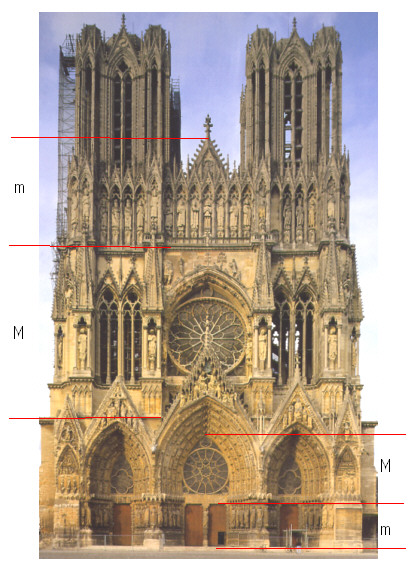
Die gotische Fassade der Kathedrale Notre-Dame in Reims

Am 6. Mai 1211 wurde der Grundstein zur neuen Kathedrale in Reims gelegt, nachdem die alte Kathedrale durch einen Brand zerstört wurde. 1285 wurden die Innenarbeiten beendet, der Nordwestturm wurde erst 1460 fertiggestellt.

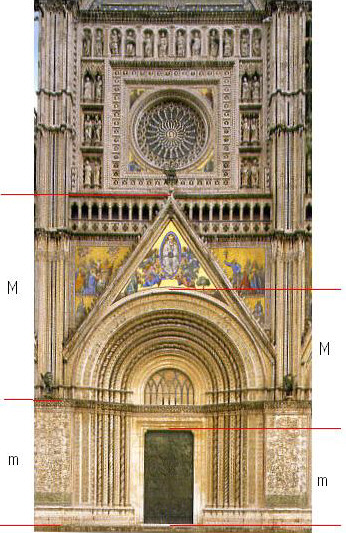
Teil der Westfassade des Doms von Orvieto

Der Dom von Orvieto ist eine dreischiffige Basilika, deren Bau Ende des 13. Jahrhunderts begonnen und deren Westfassade im 17. Jahrhundert beendet wurde.

Taj Mahal, Agra, Indien (ca.1648)                                           Nebengebäude

Beide Bauwerke sind achsensymmetrisch.

      Der Eiffelturm in Paris (1889)

Der Eiffelturm von Gustave Eiffel (1832 – 1923) wurde nach zweijähriger Bauzeit zur Weltausstellung 1889 in Paris fertiggestellt. Er war damals mit 312 m das höchste Bauwerk der Welt (heute mit Senderaufbau 324 m hoch).

(312 – 116) : 116  ≈  1,69  (ungefähr τ mit etwa 4% Abweichung)

    Sekretariatshochhaus der UNO

Die beiden führenden Architekten Oscar Niemeyer (1907 - 2012) und Le Corbusier (1887 – 1965) haben bei der Gebäudeplanung des UNO-Haupquartiers (1949 - 1953) offensichtlich den goldenen Schnitt  verwendet.

Das Sekretariatshochhaus der UNO (Bildquelle) in New York besitzt die Form eines goldenen Rechtecks:

Höhe : Breite  ≈  τ

Kirche São Francisco, Pampulha, Brasilien (1943)

Architekt war Oscar Niemeyer (1907 – 2012)

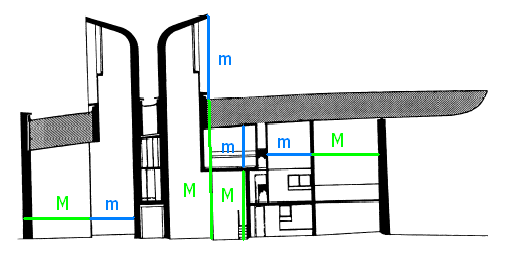
Kapelle Notre-Dame-du-Haut von Le Corbusier (1955)

  Blick von Süd-Osten

Querschnitt nach Giovanni Denti

Le Corbusier hat den goldenen Schnitt in vielfältiger Weise bei seinen Bauwerken verwendet.

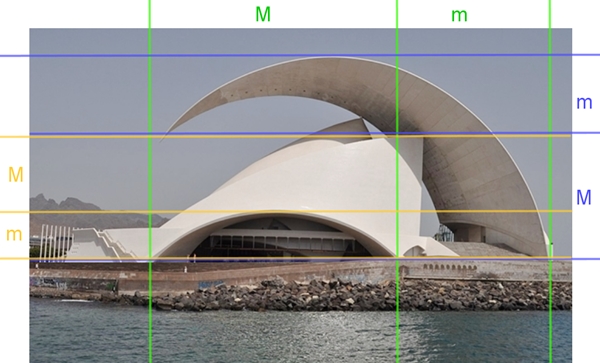
Auditorio de Tenerife, Santa Cruz, Teneriffa (2003)

Der Architekt Santiago Calatrava (geb. 1951) erhielt 1989 den Auftrag zum Bau des neuen Kongress- und Konzerthauses in Santa Cruz auf Teneriffa.

Elbphilharmonie Hamburg (2017)

Blick von Südwesten auf die Elbphilharmonie.

Die Architekten waren Jacques Herzog (geb. 1950) und Pierre de Meuron (geb. 1950).

Die Fassade wird bis zur niedrigsten Dachspitze in Näherung von einem goldenen Rechteck eingerahmt.

Daten:

rechte Dachspitze 85 m über N.N, Erdgeschossniveau 8,5 m über N.N, d.h. rechte Dachspitze 76,5 m über Bodenniveau

Plaza 37,2 m über N.N bzw. 28,7 m über Bodenniveau

Länge S-Seite 125,9 m

Berechnung:

Höhe rechte Dachspitze: Länge S-Seite = 76,5 m  : 125,9 m  ≈  0,61  ≈  σ

Höhe Plaza : Abstand zu rechter Dachspitze = 28,7 m : 47,8 m  ≈  0,60  ≈  σ

b) Beispiele in der Malerei

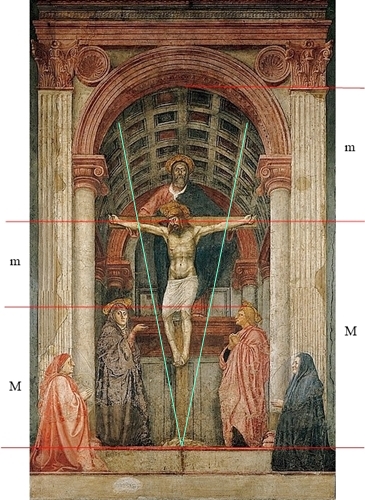
     Masaccio (1401 – 1428)

Tommaso di Ser Giovanni di Mone Cassai, genannt Masaccio, schuf zwischen 1425 und 1428 das Fresko Dreifaltigkeit in der Kirche Santa Maria Novella in Florenz. Er gilt als Begründer der Frührenaissance-Malerei. Er wandte dabei das erste Mal in der europäischen Malerei die Gesetze der Zentralperspektive richtig an. Der Fluchtpunkt der Zentralperspektive (Zentralprojektion) ist das untere Ende des Kreuzes.

Leonardo da Vinci (1452 - 1519)

Die Dame mit dem Hermelin (1486)                              Mona Lisa (1503)

Das Abendmahl (1494 - 1497, Stilrichtung: Hochrenaissance).

Das Wandgemälde befindet sich auf der Nordwand des Refektoriums des Dominikanerklosters Santa Maria delle Grazie in Mailand. Es ist 4,22 m hoch und 9,04 m breit.

Der Fluchtpunkt der Zentralperspektive (Zentralprojektion) ist die Mitte des Bildes und befindet sich im Kopf von Jesus.

Raffael (Raffaelo Santi) (1483 - 1520)

Sixtinische Madonna (1514, Stilrichtung: Hochrenaissance)

Die Schule von Athen (1510) in den Stanza della Segnatura (päpstliche Privatgemächer des Papstes Julius II), Vatikanische Museen

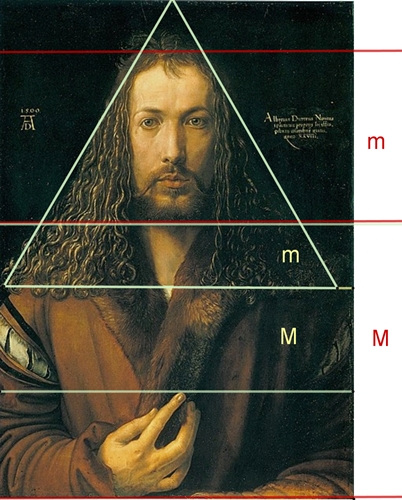
Albrecht Dürer (1471 – 1528)

Selbstbildnis im Pelzrock (1500, Stilrichtung: Renaissance)

Kopf und Haare sind von einem gleichseitigen Dreieck umrahmt.

Dürer hat 1507 die Elemente des Euklid studiert und hatte großes Wissen in Geometrie. Er kannte den goldenen Schnitt.

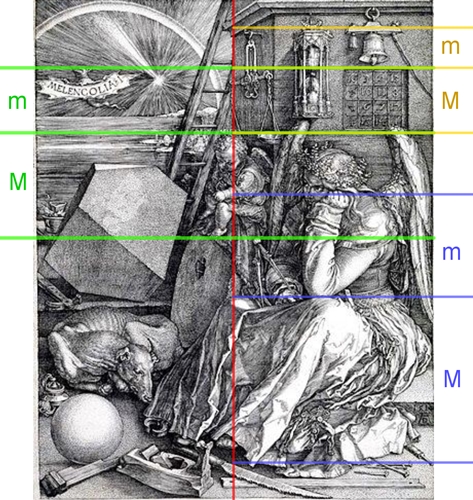
Melencolia I (Kupferstich von 1514, mit einem magischen Quadrat)

Caspar David Friedrich (1774 – 1840)

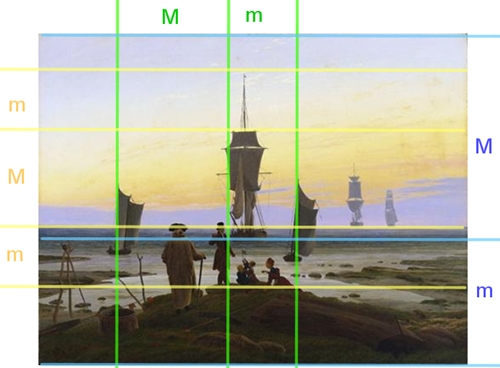
Die Lebensstufen (um 1835, Stilrichtung: Frühromantik)

John Constable (1776 – 1837)

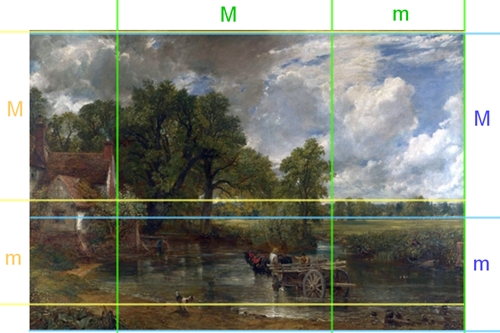
Der Heuwagen (1821, Stilrichtung: Romantik)

Georges-Pierre Seurat (1859 – 1891)

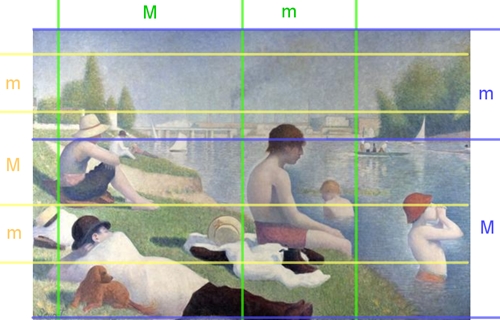
Badestelle in Asnières (1883/1884, Stilrichtung: Pointillismus)

Claude Monet (1840 – 1926)

Heuhaufen in Giverny (1886, Stilrichtung Impressionismus)

Vincent van Gogh (1853 – 1890)

Frau, im Gras sitzend (1887, Stilrichtung: Neoimpressionismus)

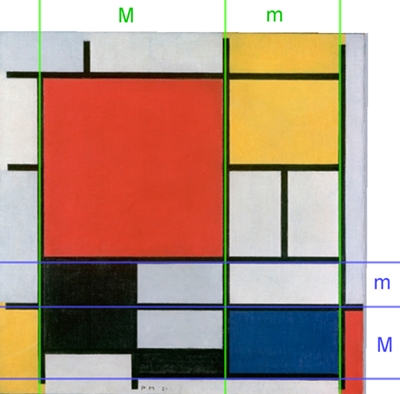
Piet Mondrian (1872 – 1944)

Komposition mit Rot, Gelb, Blau und Schwarz (1921, Stilrichtung: abstrakte Malerei)

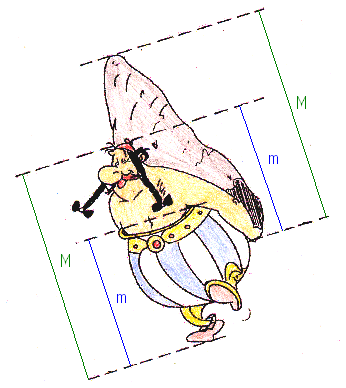
Albert Uderzo (1927 - 2020)

Obelix, gezeichnet von Albert Uderzo in Asterix-Bänden seit 1961

c) Beispiele in der Musik

Es wird behauptet, dass auch Komponisten den goldenen Schnitt in Kompositionen verwendet haben, z. B. Bach, Mozart, Schubert, Debussy, Satie, Bartok. 

In der Musik kann der goldene Schnitt in zwei Formen auftreten. Einerseits können zwei Töne zueinander in der Proportion des goldenen Schnitts stehen, andererseits kann die Komposition eines Stückes aus Teilen bestehen, deren Längen sich zueinander im goldenen Schnitt verhalten. 

Bei  W. A. Mozart wurde die Vermutung geäußert, dass er den goldenen Schnitt in der Sonatensatzform seiner Klaviersonaten (meist 1. Satz) verwendet hat. Die Sonatensatzform besteht aus 2 Teilen:
1. Teil:  Exposition
2. Teil:  Durchführung und Reprise

In folgender Tabelle sind in der ersten Spalte unter KV das Köchelverzeichnis der entsprechenden Klaviersonate mit Sonatensatzform, in der 2. Spalte die Anzahl der Takte des 1. Teils, in der 3. Spalte die Anzahl der Takte des 2. Teils und in der 4. Spalte der Quotient aus 2. und 3. Spalte angegeben.