|
Die
17 Symmetriegruppen eines ebenen periodischen Musters
Dafür verwendet man auch die
Bezeichnungen ebene kristallographische Gruppen, Wandmustergruppen,
Tapetengruppen (E: wallpaper groups).
Alle 17
Symmetriegruppen enthalten
Verschiebungen, zusätzlich
Drehungen,
Spiegelungen
und/oder
Gleitspiegelungen.
Die
Symmetriegruppe eines ebenen periodischen Musters besitzt folgende Untergruppen:
a)
Die
Translationsgruppe, die von zwei linear unabhängigen Vektoren (grün und blau)
erzeugt werden.
b)
Die
zyklischen Gruppen der Ordnung 1, 2, 3, 4 oder 6. Sie stellen jeweils
Drehungen um 360° , 180° (zweizählige Rotation), 120° (dreizählige
Rotation), 90° (vierzählige Rotation) oder 60° (sechszählige Rotation).
c)
Die
Diedergruppe der Ordnung 2, 4, 6, 8 oder 12.
Jedes periodische Muster kann dadurch erzeugt
werden, dass auf eine Elementarzelle obige Operationen immer wieder angewandt
werden. Dabei wird die Ebene parkettiert.
Die in den Mustern angegebenen Elemente sind wie
folgt gekennzeichnet:
|

|
Drehzentrum einer zweizähligen Rotation (180°).
|
|

|
Drehzentrum einer dreizähligen Rotation (120°).
|
|

|
Drehzentrum einer vierzähligen Rotation
(90°).
|
|

|
Drehzentrum einer sechszähligen Rotation (60°).
|
|

|
Spiegelachse.
|
|

|
Gleitspiegelachse.
|
Unterschiedliche Äquivalenzklassen (Klassen) von
Elementen werden durch senkrechte Striche „|“ getrennt.
Die gelb markierten Fläche kennzeichnet eine
Elementarzelle.
Die translative
Zelle (Parkettstein) bildet den Fundamentalbereich für die Translationsgruppe.
Ab
Gruppe p3 (13. Fall) kann die translative
Zelle entweder ein regelmäßiges Sechseck oder eine Raute mit einem 60°-Winkel
sein.
Die 17 Symmetriegruppengruppen eines ebenen
periodischen Musters:
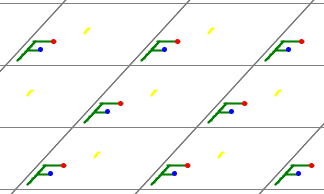
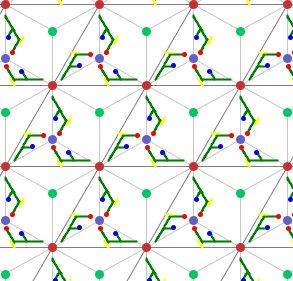
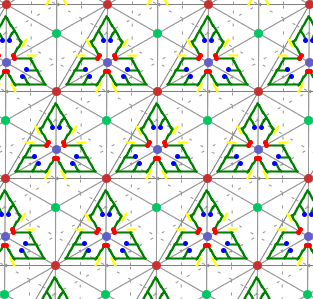
Links jeweils die grundlegende Struktur, rechts ein Beispielbild.
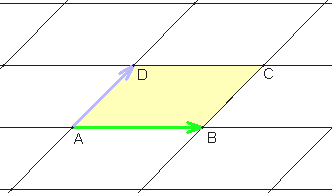
1) Gruppe p1
Sie besitzt nur die Translationsgruppe.
Die Elementarzelle ist gleich der translativen Zelle (Parallelogramm).
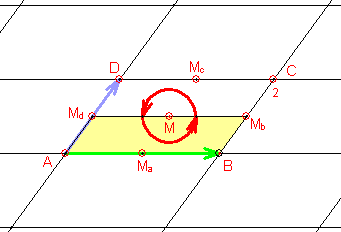
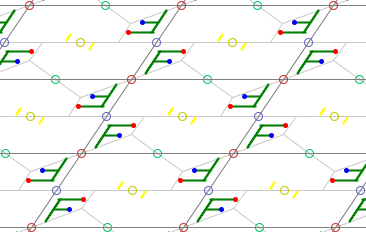
2) Gruppe p2
Sie besitzt zusätzlich zur Translationsgruppe vier Klassen zweizähliger
Rotationen
mit Drehzentren: A, B, C, D
|
M |
Ma, Mc
|
Mb, Md.
Die Elementarzelle ist halb so groß wie die translative Zelle (Parallelogramm).
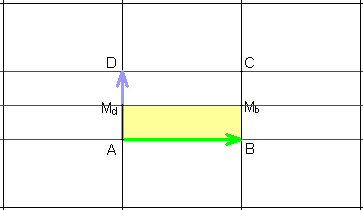
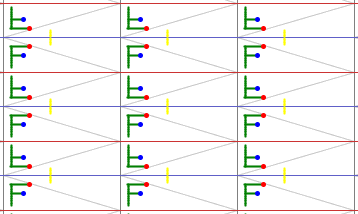
3) Gruppe pm
Sie besitzt zusätzlich zur Translationsgruppe zwei Klassen zueinander
paralleler Spiegelachsen:
AB, DC |
MdMb.
Die Elementarzelle ist halb so groß wie die translative Zelle (Rechteck).
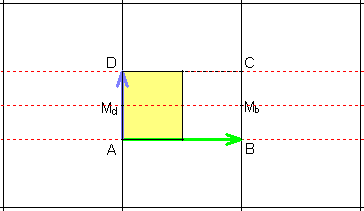
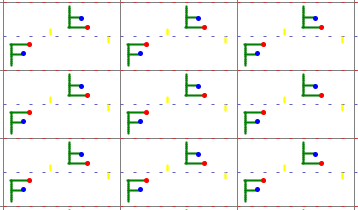
4) Gruppe pg
Sie besitzt zusätzlich zur Translationsgruppe zwei Klassen zueinander
paralleler Gleitspiegelachsen:
AB,
CD
|
MdMb.
Die Elementarzelle ist halb so groß wie die translative Zelle (Rechteck).
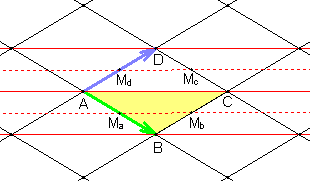
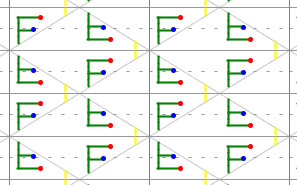
5) Gruppe cm
Sie besitzt zusätzlich zur Translationsgruppe abwechselnd eine Klasse
paralleler Spiegelachsen und Gleitspiegelachsen.
Die Elementarzelle ist halb so groß wie die translative Zelle (Raute).
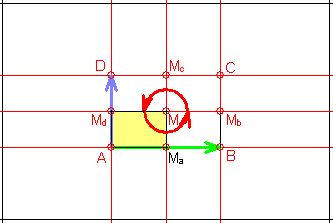
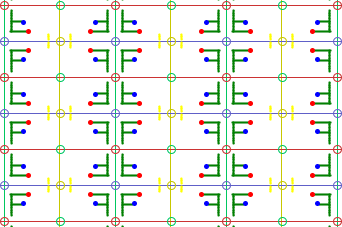
6) Gruppe pmm
Sie besitzt zusätzlich zur Translationsgruppe vier Klassen zueinander
senkrechter Spiegelachsen:
AB, DC
|
AD, BC
|
MdMb
|
MaMc.
In deren Schnittpunkten befinden sich vier Klassen zweizähliger Rotationen mit
Drehzentren: A, B, C, D
|
M
|
Ma, Mc
|
Mb, Md.
Die Elementarzelle ist ein Viertel so groß wie die translative Zelle (Rechteck).
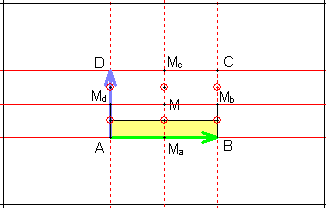
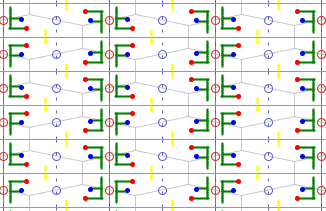
7) Gruppe pmg
Sie besitzt zusätzlich zur Translationsgruppe jeweils eine Klasse von
Spiegelachsen und zwei Klassen dazu senkrechter Gleitspiegelachsen: AD, BC
|
MaMc
Auf den Gleitspiegelachsen befinden sich jeweils zwei Klassen zweizähliger
Rotationen mit den Drehzentren: In der Mitte von [AMd], [MdD],
[BMb], [MbC] |
[MaM], [MMc].
Die Elementarzelle ist ein Viertel so groß wie die translative Zelle (Rechteck).
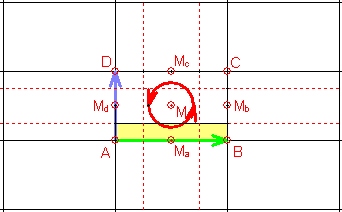
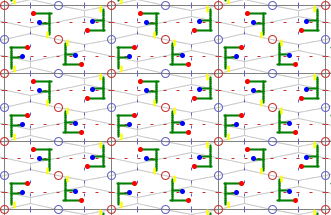
8) Gruppe pgg
Sie besitzt zusätzlich zur Translationsgruppe zwei Klassen zueinander
senkrechter Gleitspiegelachsen und zwei Klassen von zweizähligen Rotationen mit
den Drehzentren:
A, B, C, D, M
|
Ma, Mb, Mc, Md.
Die Elementarzelle ist ein Viertel so groß wie die translative Zelle (Rechteck).
9)
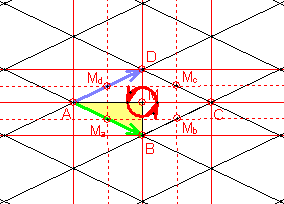
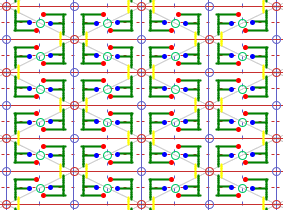
Gruppe cmm
Sie besitzt zusätzlich zur Translationsgruppe jeweils zwei Klassen von
Spiegelachsen und Gleitspiegelachsen:
AC und Parallelen |
BD und
Parallelen.
In deren Schnittpunkten befinden sich jeweils drei Klassen von zweizähligen
Rotationen mit den Drehzentren:
A,
B, C, D
|
Ma, Mb, Mc, Md
|
M.
Die Elementarzelle ist ein Viertel so groß wie die translative Zelle (Raute).
10)
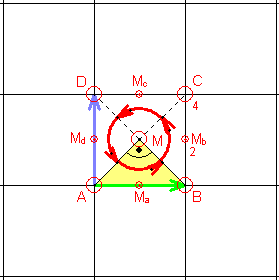
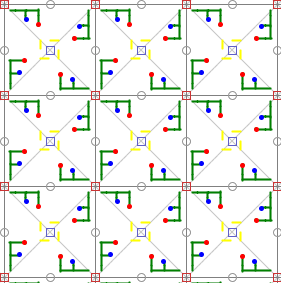
Gruppe p4
Sie besitzt zusätzlich zur Translationsgruppe zwei Klassen vierzähliger
Rotationen mit den Drehzentren:
A,
B, C, D
|
M.
Dazwischen liegt eine Klasse zweizähliger Rotationen mit den Drehzentren:
Ma, Mb, Mc, Md
.
Die Elementarzelle ist ein Viertel so groß wie die translative Zelle (Quadrat).
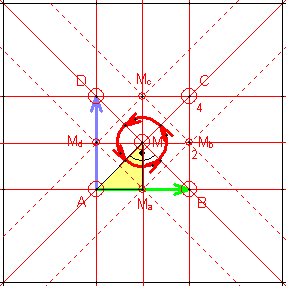
11) Gruppe p4m (p4mm)
Sie besitzt zusätzlich zur Translationsgruppe zwei Klassen vierzähliger
Rotationen mit den Drehzentren:
A,
B, C, D
|
M.
Dazwischen liegt eine Klasse zweizähliger
Rotationen mit den Drehzentren:
Ma,
Mb, Mc, Md
.
Außerdem besitzt sie 3 Klassen von Spiegelachsen: AB, BC, CD, AD
|
AC, BD
|
MaMc, MbMd
Schließlich gibt es noch eine Klasse von Gleitspiegelachsen.
Die Elementarzelle ist ein Achtel so groß wie die translative Zelle (Quadrat).
 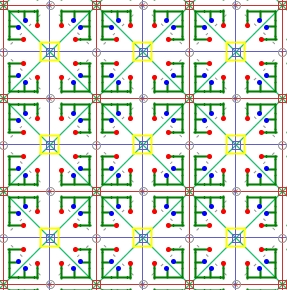
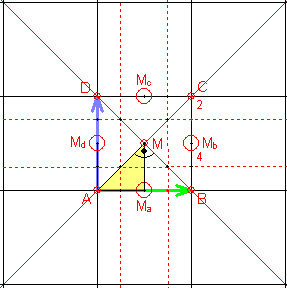
12) Gruppe p4g (p4gm)
Sie besitzt zusätzlich zur Translationsgruppe jeweils eine Klasse zweizähliger
und vierzähliger Rotationen. Außerdem besitzt sie jeweils eine Klasse von
Spiegelachsen und
Gleitspiegelachsen.
Die Elementarzelle ist ein Achtel so groß wie die translative Zelle (Quadrat).
 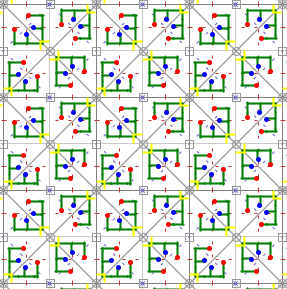
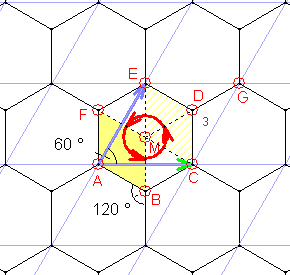
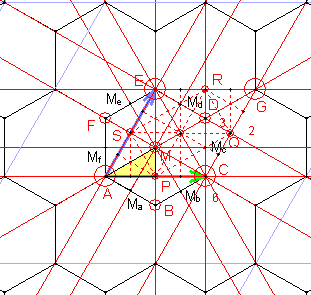
13)
Gruppe p3
Sie besitzt zusätzlich zur Translationsgruppe drei Klassen dreizähliger
Rotationen mit den Drehzentren:
A,
C, G, E
|
B, D, F
|
M.
Die Elementarzelle ist ein Drittel so groß wie die translative Zelle
(Regelmäßiges Sechseck oder Raute mit 60°-Winkel).
14)
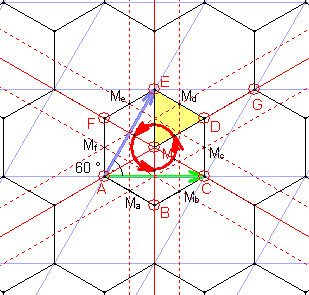
Gruppe p3m1
Sie besitzt zusätzlich zur Translationsgruppe drei Klassen
dreizähliger Rotationen mit den Drehzentren:
A, C, G, E
|
B, D, F
|
M.
Außerdem gibt es jeweils eine Klasse von Spiegelachsen und Gleitspiegelachsen.
Die Elementarzelle ist ein Sechstel so groß wie die translative Zelle
(Regelmäßiges Sechseck oder Raute mit 60°-Winkel).
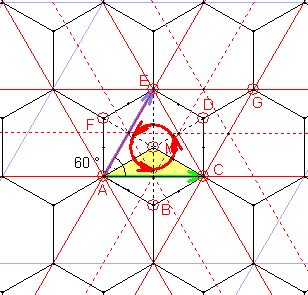
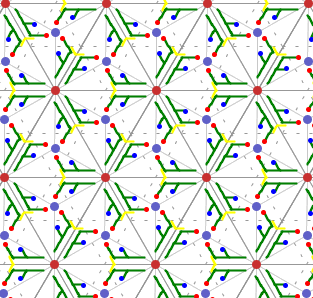
15) Gruppe p31m
Sie besitzt zusätzlich zur Translationsgruppe zwei Klassen dreizähliger
Rotationen mit den Drehzentren: A, C, G, E
|
B, D, F, M.
Außerdem besitzt sie jeweils eine Klasse von
Spiegelachsen und Gleitspiegelachsen.
Die Elementarzelle ist ein Sechstel so groß wie die translative Zelle
(Regelmäßiges Sechseck oder Raute mit 60°-Winkel).
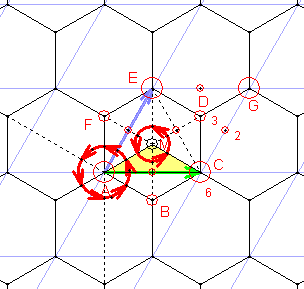
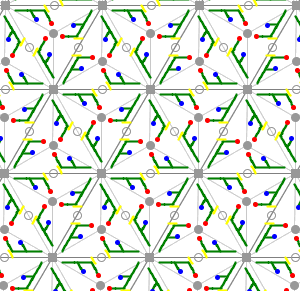
16)
Gruppe p6
Sie besitzt zusätzlich zur Translationsgruppe jeweils eine Klasse zweizähliger,
dreizähliger und sechszähliger Rotationen.
Die Elementarzelle ist ein Sechstel so groß wie die translative Zelle
(Regelmäßiges Sechseck oder Raute mit 60°-Winkel).
17) Gruppe p6m (p6mm)
Sie besitzt zusätzlich zur Translationsgruppe jeweils eine Klasse zweizähliger,
dreizähliger und sechszähliger Rotationen. Außerdem besitzt sie 2 Klassen von
Spiegelachsen: AC, CG, EG, AE, CE
|
BE, CF, AD.
Es gibt auch noch 2 Klassen von Gleitspiegelachsen: PQ, QR, RS, PS, QS, PR
|
Rest
Die Elementarzelle ist ein Zwölftel so groß wie die translative Zelle.
Die Konstruktionen wurden mit dem Programm Dynageo von R. Mechling
durchgeführt:
http://www.dynageo.de/
Die Beispielbilder wurden mit einem Javaprogramm von Martin von Gagern
gefertigt:
https://www.imaginary.org/de/program/morenaments
Weiteres Javaprogramm zum Erzeugen von Bildern:
http://www.geom.uiuc.edu/java/Kali/
Die
Symmetriegruppen eines ebenen periodischen Musters in der
maurischen Ornamentik
Fotos von M. Holzapfel, aufgenommen im Alcázar (Sevilla) und in der Alhambra
(Granada):
Beispiel
für die Gruppe pm: Beispiel für die Gruppe p3:
 
Beispiel
für die Gruppe cmm
(ohne Berücksichtigung der Farbe):

Beispiele
für die Gruppe p4:
 
Beispiele
für die Gruppe p4m:
 

Aus
der Ferne betrachtet: p4m
Aus der Nähe betrachtet:
p4;
die schmalen weißen Bänder überdecken sich und schließen damit die Achsensymmetrie aus.
Beispiel
für die Gruppe
p6: Beispiel für die Gruppe p6m
(ohne Farben):
 

Aus
der Ferne betrachtet: p6m
Aus der Nähe betrachtet:
p6;
die schmalen weißen Bänder überdecken sich und schließen damit die Achsensymmetrie aus.
Die
Symmetriegruppen in den Grafiken von M. C.
Escher
Escher
studierte 1926 und dann vor allem 1936 die maurische Ornamentik in der Alhambra.
15 der 17 Symmetriegruppen sind in den Werken von
M. C. Escher zu erkennen.
Tiled.Art, Galerie von Escher-ähnlichen Figuren
mit Animation und Zuordnung zu den 17 Symmetriegruppen:
Tessellations, Escher-style - Tiled.art
Bilder von Escher: M.
C. Escher - 470 Kunstwerke - Druck (wikiart.org)
Zurück
Zurück zur Startseite
| 











































