|
Der Würfel - das Hexaeder
Der Würfel besitzt als Oberfläche 6
kongruente Quadrate 12 gleich lange Kanten und 8 Eckpunkte.
Berechnung des
In- und Umkugelradius r des Würfels mit der Kantenlänge a: 
Länge d der
Diagonale eines Quadrats der Seitenlänge a:
d² = a² + a²
(Pythagoras)
d = a
√2
Länge e der
Raumdiagonale des Würfels
e² = a² + d²
(Pythagoras)
e² = 3 a² oder e = a
√3
Umkugelradius R des Würfels: R = e/2 = 1/2
√3
a ≈ 0,866 a
Inkugelradius r des Würfels: r = a/2 = 0,5 a
In- und Umkugel des Würfels 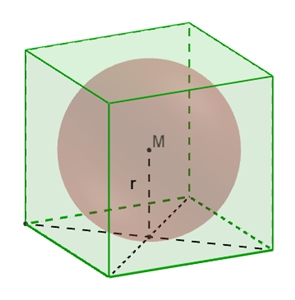
Oberflächen- und Volumeninhalts des
Würfels:
Der Würfel besitzt als Oberfläche 6 gleich
große Quadrate mit dem Flächeninhalt a2.
Oberflächeninhalt O des Würfels: O = 6 a²
Volumeninhalt
V des Würfels: V = a³
Winkel im Würfel:
Innenwinkel α des Quadrats: α =
90°.
Winkel β zwischen benachbarten
Flächen des Würfels: β = 90°
Winkel γ zwischen Kante und
Fläche eines Würfels: γ = 90° |
