Eigenschaften platonischer Körper

Die fünf platonischen Körper

Körper, die von Flächen begrenzt werden, heißen Polyeder (griech.: Vielflach). Die bekanntesten Polyeder sind Quader, Prisma und Pyramide.

Platonische Körper sind  reguläre konvexe Polyeder, das heißt, die begrenzenden Vielecke sind regelmäßig und gleich groß. In jeder Ecke des Körpers treffen jeweils gleich viele und gleich lange Kanten zusammen, an jeder Kante treffen sich zwei deckungsgleiche Flächen.

Es gibt nur fünf - nach dem griechischen Philosophen Platon benannte -  verschiedene platonische Körper:

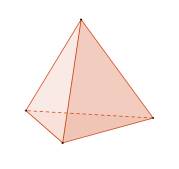
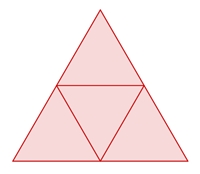
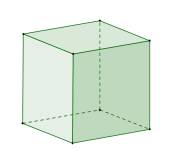
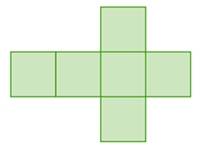
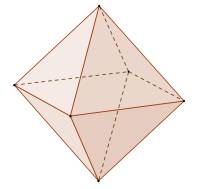
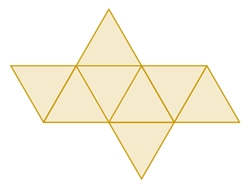
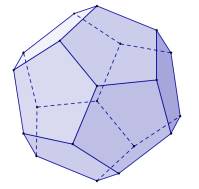
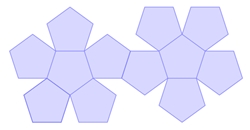
             Tetraeder                           Hexaeder (Würfel)                         Oktaeder                               Dodekaeder                              Ikosaeder

Netze dazu:

 
Polyedersatz von Euler:   e + f = k + 2    (Leonard Euler 1707-1783)

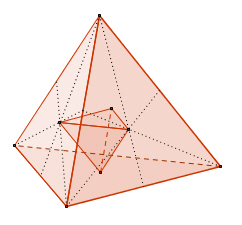
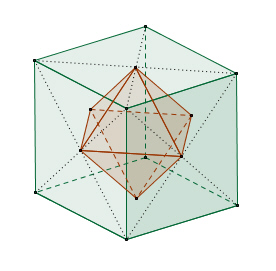
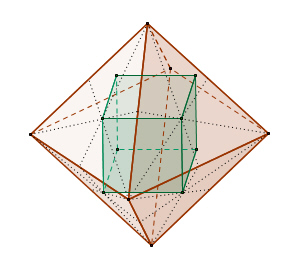
Die Dualität platonischer Körper

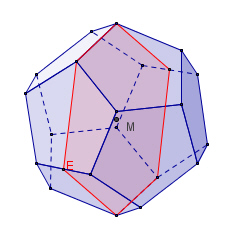
Wenn man die Mittelpunkte zweier benachbarter Seitenflächen eines platonischen Körpers verbindet, erhält man wieder einen platonischen Körper mit demselben Mittelpunkt. Dieser Körper wird als Dualkörper zum Ausgangskörper bezeichnet. Dabei wird die Anzahl der Flächen mit der Anzahl der Ecken vertauscht, während die Anzahl der Kanten gleich bleibt.

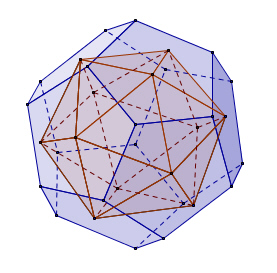
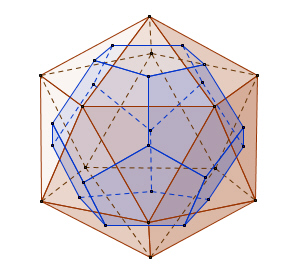
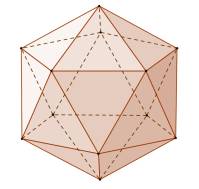
Ikosaeder und goldenes Rechteck

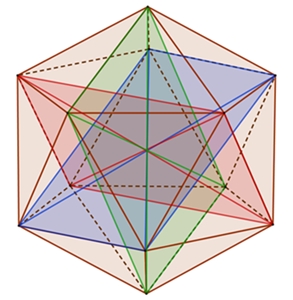
Im Ikosaeder befinden sich 3 zueinander senkrechte goldene Rechtecke mit einem gemeinsamen Mittelpunkt.

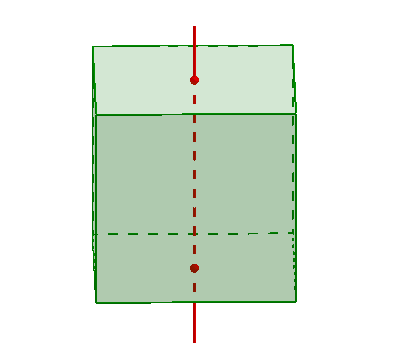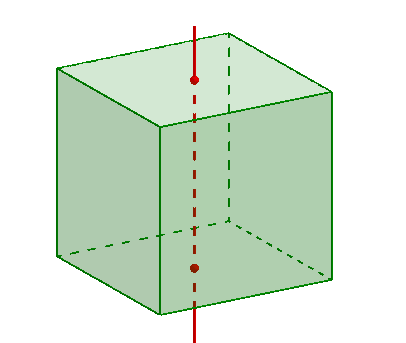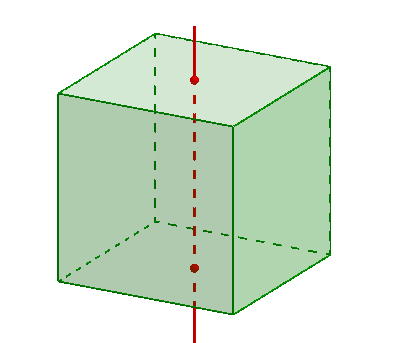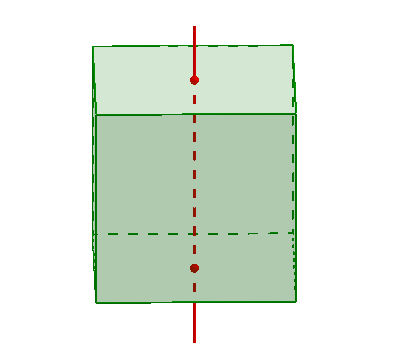
Die Symmetrie platonischer Körper

Folgende Symmetriearten kann es bei einem platonischen Körper geben:

• Rotationssymmetrie bezüglich einer Drehachse mit mindestens zweizähliger Drehachse,

• Symmetrie bezüglich einer Ebene,

• Symmetrie bezüglich eines Punktes.
  

Es gilt:

• Ein Körper ist rotationssymmetrisch mit n-zähliger Drehachse, wenn eine Drehung um 360°/n den Körper auf sich selbst abbildet.

• Eine Ebene E ist Symmetrieebene, wenn der Körper bei Spiegelung an E auf sich selbst abbildet wird.

• Ein Körper ist punktsymmetrisch zu P (symmetrisch bezüglich des Punktes P), wenn der Körper bei Spiegelung an P auf sich selbst abbildet wird.

Symmetrie des Tetraeders:

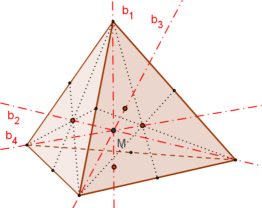
Das Tetraeder besitzt

3 zweizählige Drehachsen a durch die Mittelpunkte gegenüberliegender Kanten,

4 dreizählige Drehachsen b durch die Ecken und die Mitten der gegenüberliegenden Seitenflächen,

6 Symmetrieebenen E jeweils durch eine Kante und den Mittelpunkt der gegenüberliegenden Kante,

keine Punktsymmetrie.
  

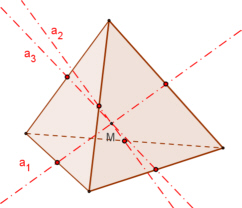
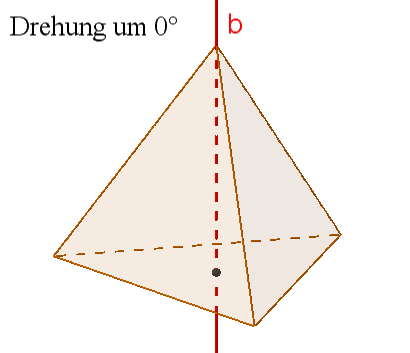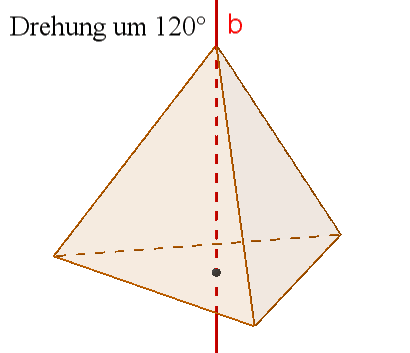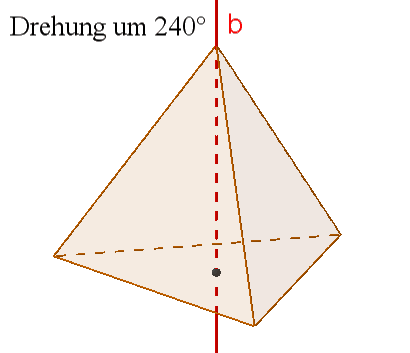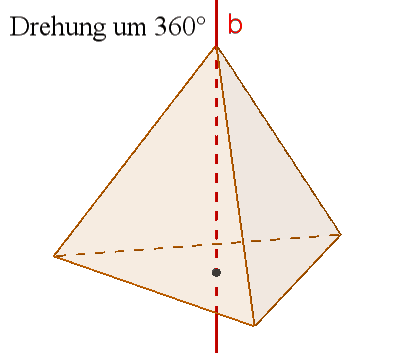
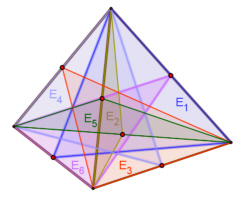
Damit besitzt das Tetraeder 3*1 + 4*2 + 1 ( Identität ¹⁾) = 12  verschiedene Abbildungen der Drehgruppe. Diese 12 Elemente der Drehgruppe kombiniert mit den 6 Ebenenspiegelungen und 6 Drehspiegelungen ergeben  24 Abbildungen, die die Bedingungen einer Gruppe erfüllen und die sog. Tetraedergruppe bilden.

¹⁾  Identität (identische Abbildung) = Drehung um 360°

Symmetrie des Hexaeders und Oktaeders:

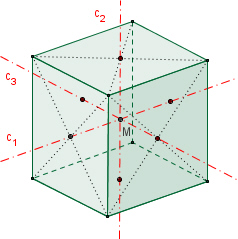
Das Hexaeder besitzt

6 zweizählige Drehachsen a durch die Mittelpunkte gegenüberliegender Kanten,
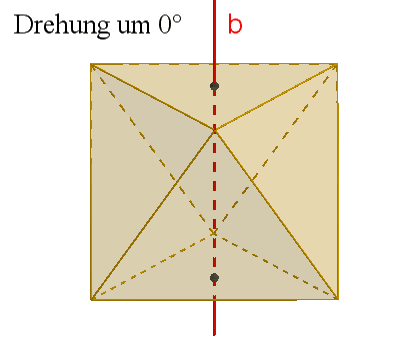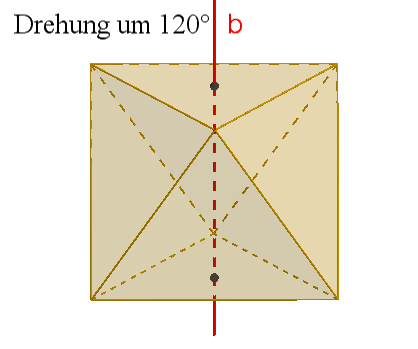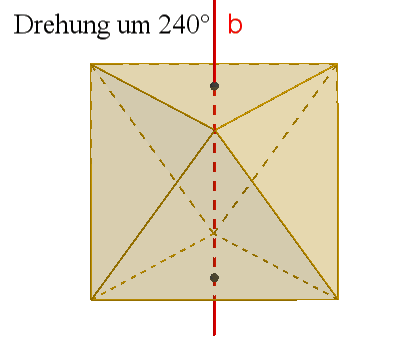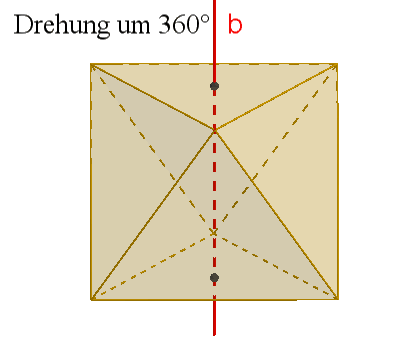
4 dreizählige Drehachsen b durch gegenüberliegende Ecken,
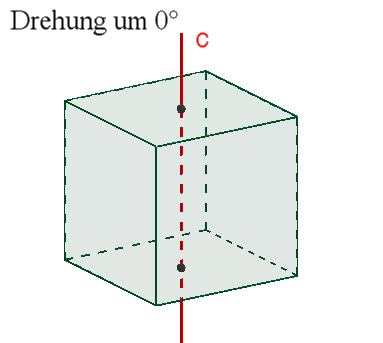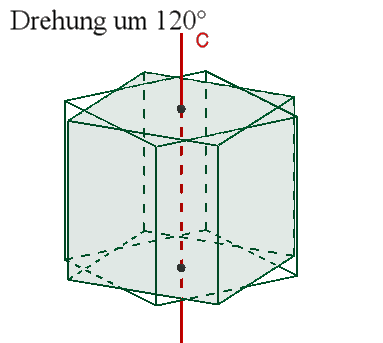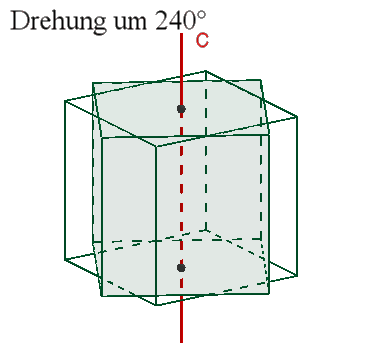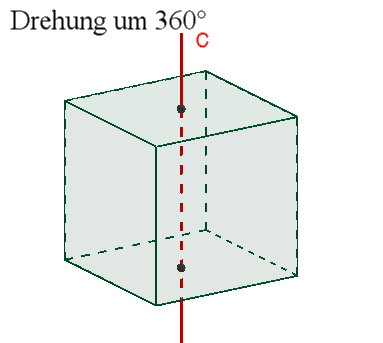
3 vierzählige Drehachsen c durch die Mittelpunkte gegenüberliegender Flächen,
9 Symmetrieebenen E, jeweils drei Ebenen durch je vier Ecken, sechs Ebenen durch jeweils zwei Ecken und zwei Kantenmittelpunkte,
1 Punktsymmetrie zum Mittelpunkt.
 

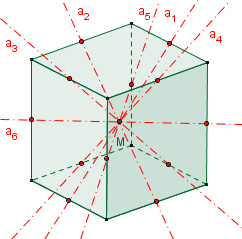
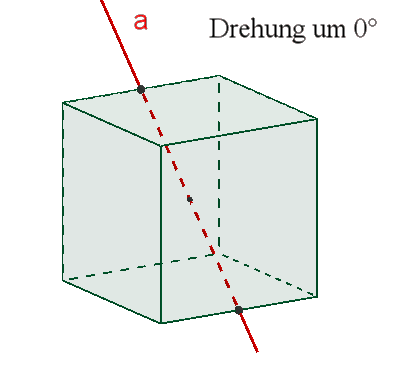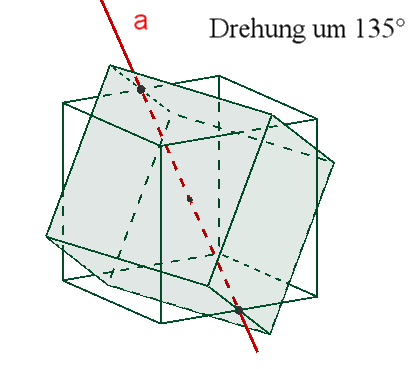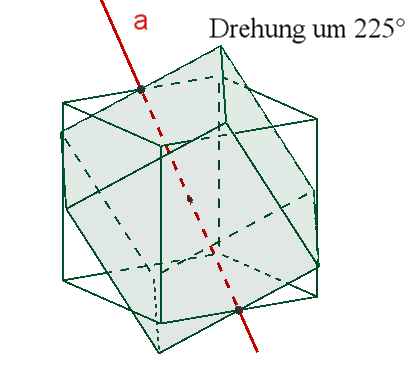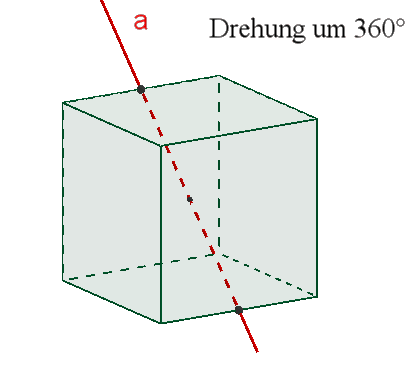
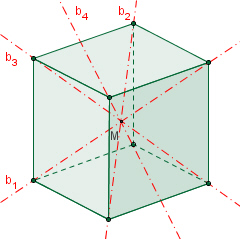
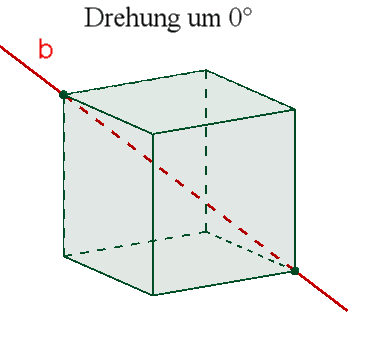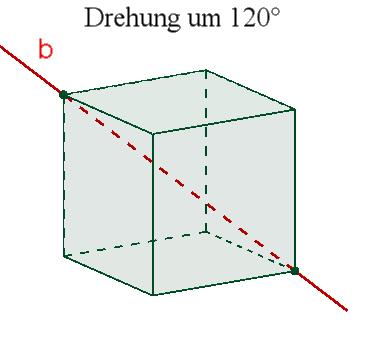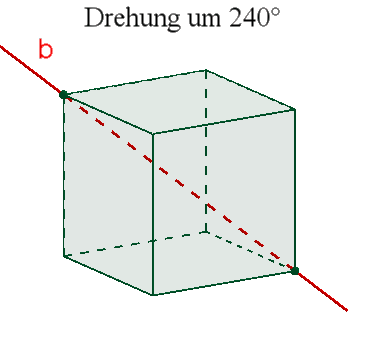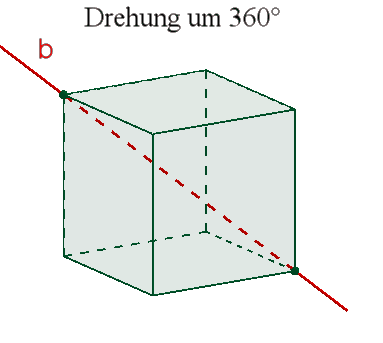
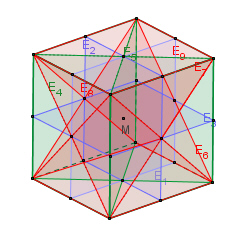
Das Oktaeder besitzt wie das Hexaeder

6 zweizählige Drehachsen a durch die Mittelpunkte gegenüberliegender Kanten,
4 dreizählige Drehachsen b durch gegenüberliegende Ecken,
3 vierzählige Drehachsen c durch die Mittelpunkte gegenüberliegender Flächen,
9 Symmetrieebenen E, jeweils drei Ebenen durch je vier Ecken, sechs Ebenen durch jeweils zwei Ecken und zwei Kantenmittelpunkte,
1 Punktsymmetrie zum Mittelpunkt.

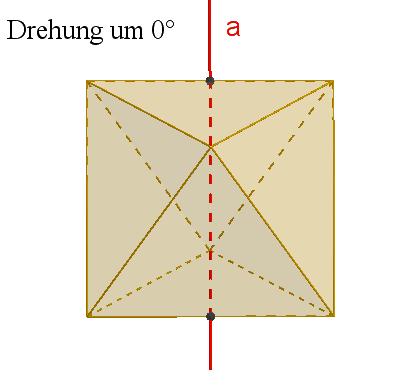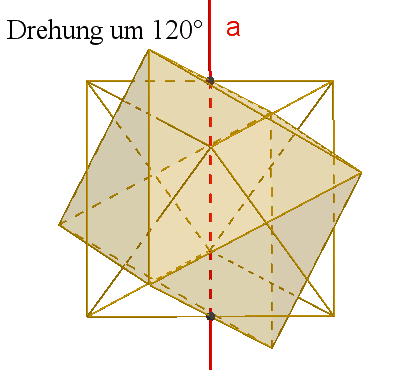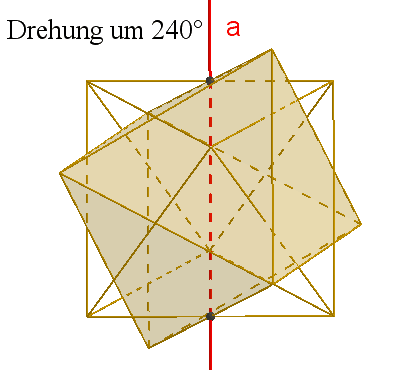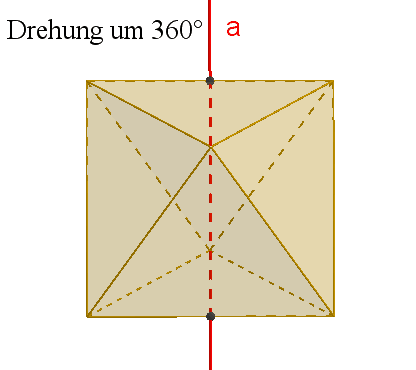
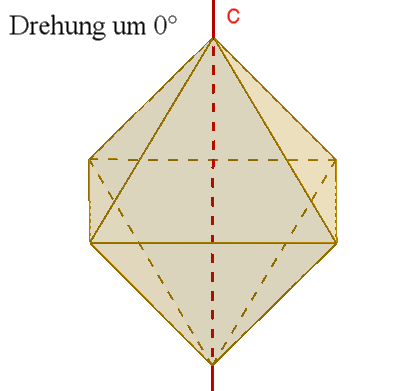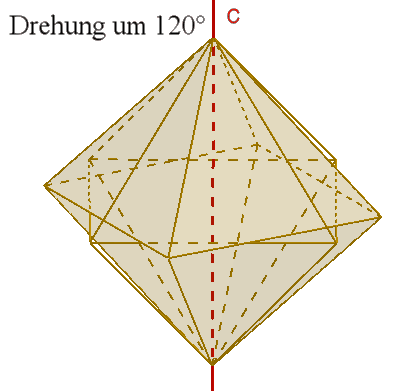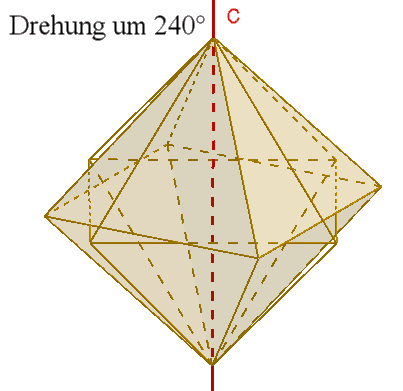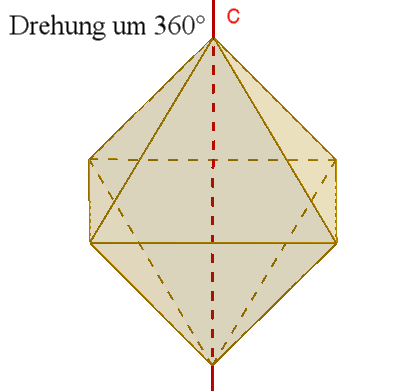
Damit besitzt das Hexaeder als Gruppenelemente 6*1 + 4*2 + 3*3 + 1(Identität) = 24  verschiedene Abbildungen der Drehgruppe. Diese 24 Elemente der Drehgruppe kombiniert mit den Ebenenspiegelungen und Drehspiegelungen ergeben  48 Abbildungen, die die sog. Hexaedergruppe bilden.
Wegen der Dualität gilt:

Hexaedergruppe = Oktaedergruppe.

Sie besitzen jeweils 48 Elemente.

Die Tetraedergruppe ist eine Untergruppe der Hexaedergruppe.
 

Symmetrie des Dodekaeders und Ikosaeders:

Das Dodekaeder besitzt

15 zweizählige Drehachsen a durch die Mittelpunkte gegenüberliegender Kanten,
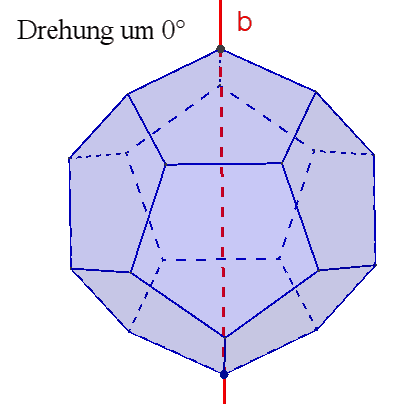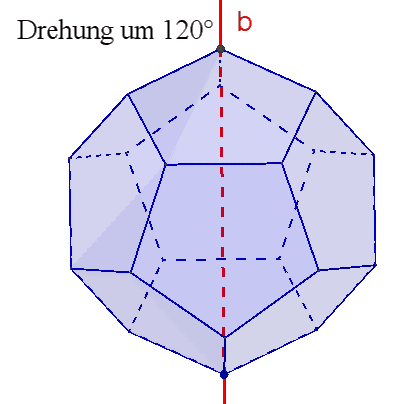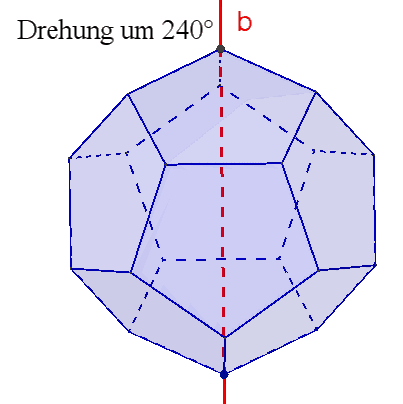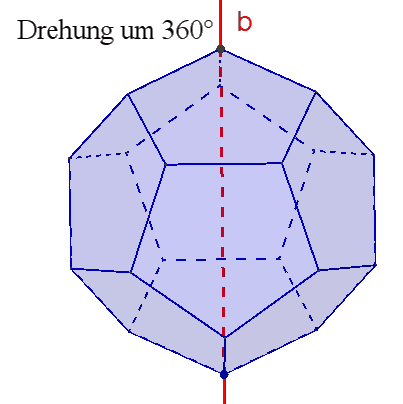
10 dreizählige Drehachsen b durch gegenüberliegende Ecken,
6 fünfzählige Drehachsen durch gegenüberliegende Flächenmittelpunkte,
15 Symmetrieebenen durch gegenüberliegende, parallele Kanten,
1 Punktsymmetrie zum Mittelpunkt.

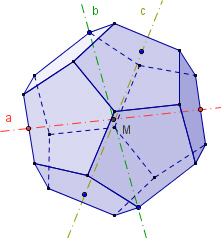
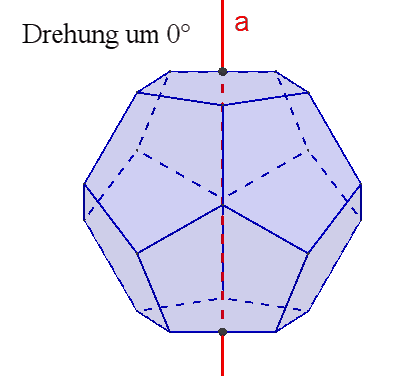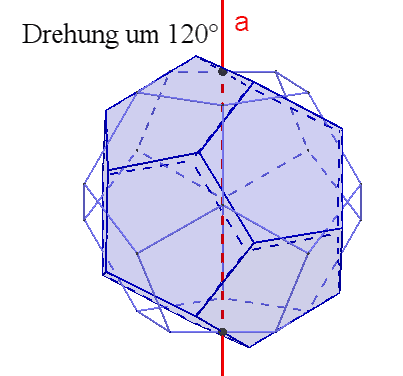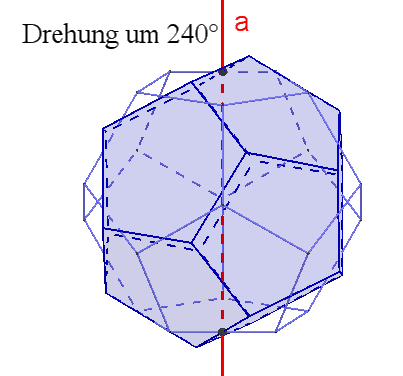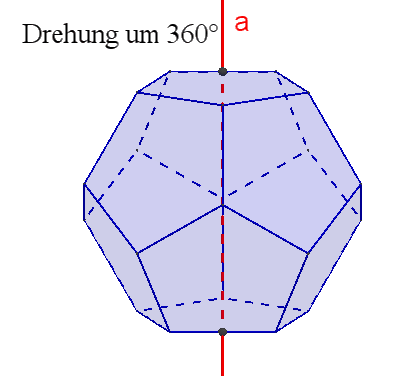
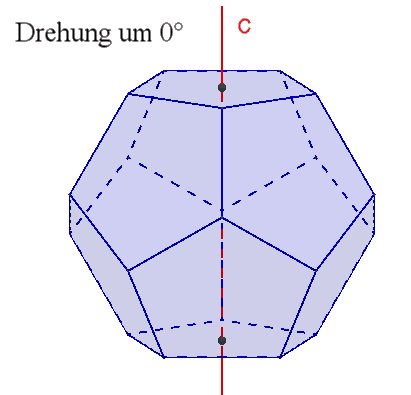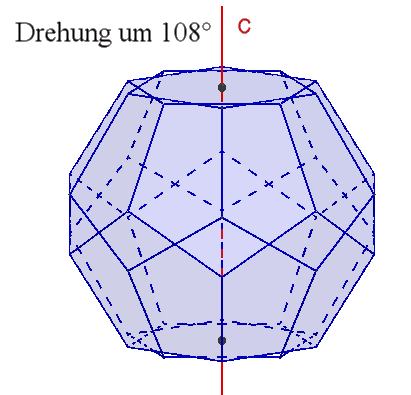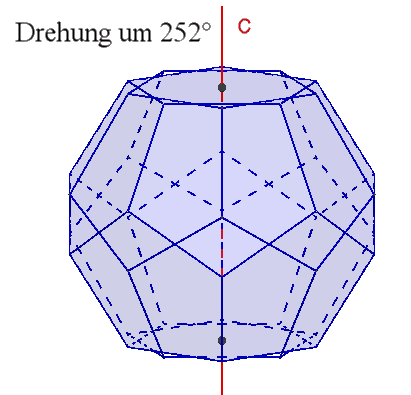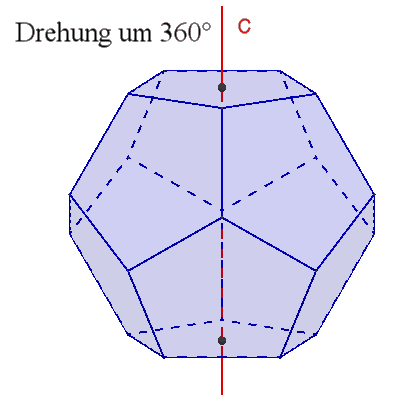
Damit besitzt das Dodekaeder als Gruppenelemente 15*1 + 10*2 + 6*4  + 1 (Identität) = 60  verschiedene Abbildungen der Drehgruppe. Diese 60 Elemente der Drehgruppe kombiniert mit den Spiegelungen ergeben 2*60 = 120 Abbildungen, die die sog. Dodekaedergruppe bilden.

Wegen der Dualität gilt:

Dodekaedergruppe = Ikosaedergruppe.

Sie besitzen jeweils 120 Elemente.

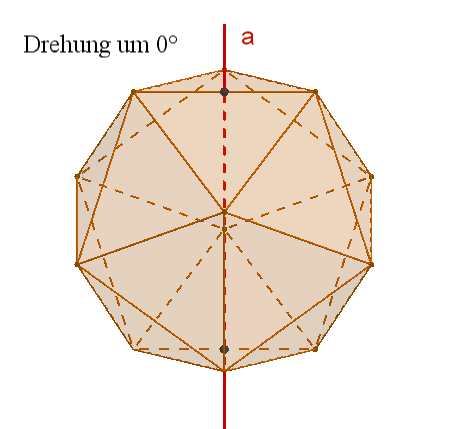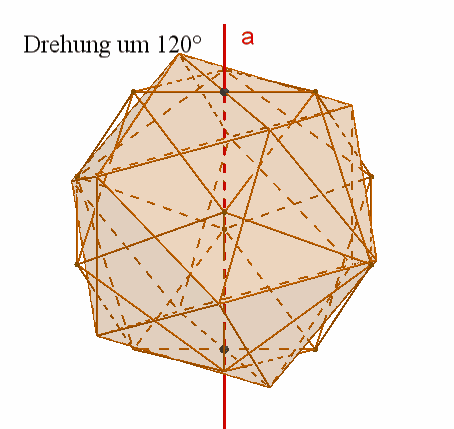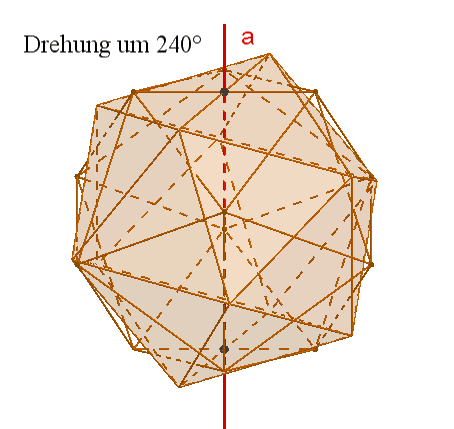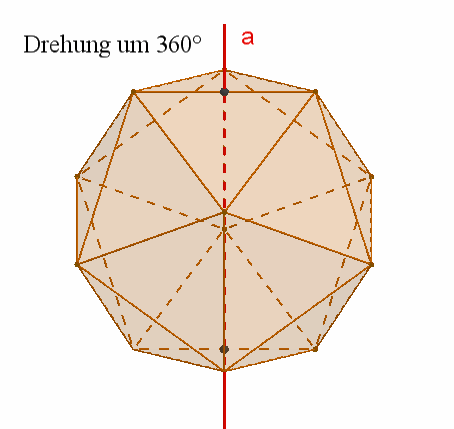
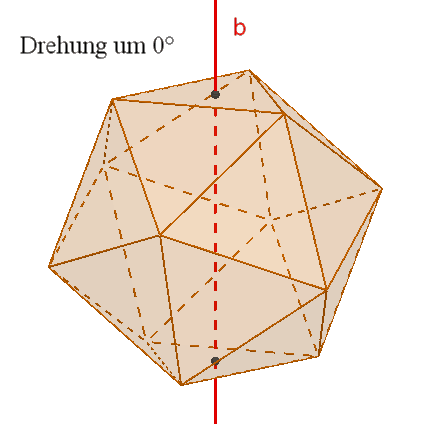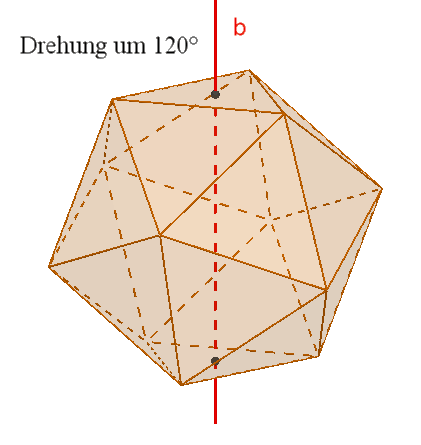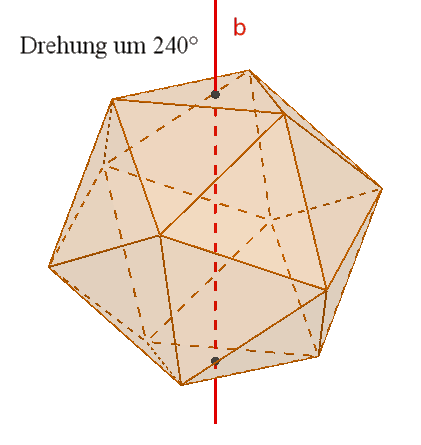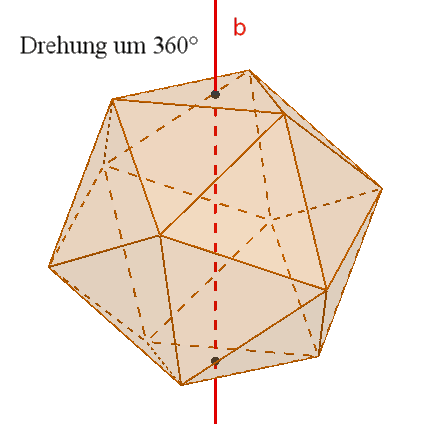
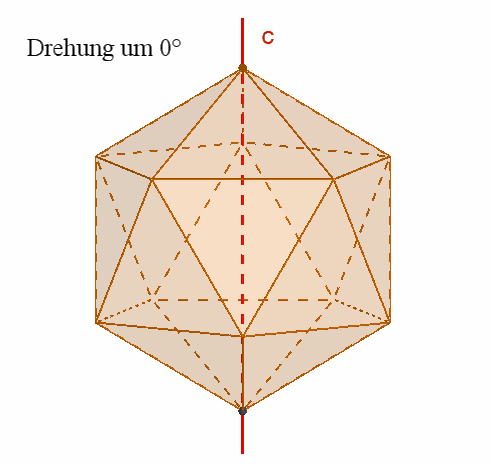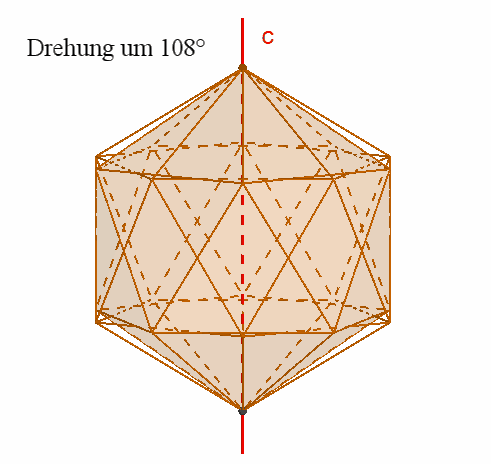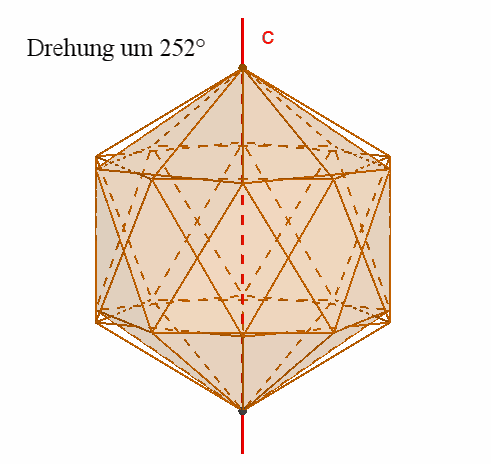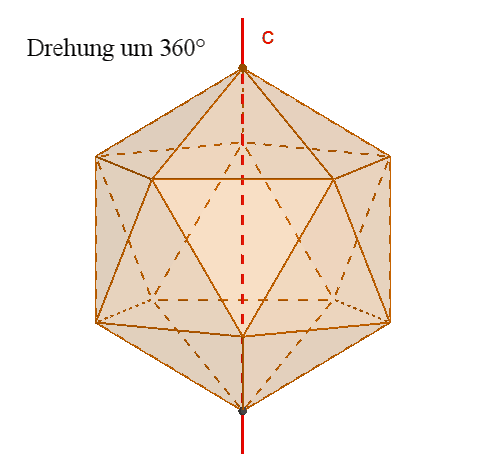
Das Ikosaeder besitzt wie das Dodekaeder

15 zweizählige Drehachsen a durch die Mittelpunkte gegenüberliegender Kanten,
10 dreizählige Drehachsen b durch gegenüberliegende Ecken,
6 fünfzählige Drehachsen durch gegenüberliegende Flächenmittelpunkte,
15 Symmetrieebenen durch gegenüberliegende, parallele Kanten,
1 Punktsymmetrie zum Mittelpunkt.

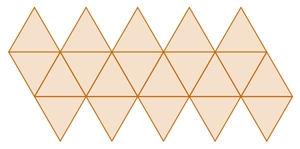
Parkettierung des Raumes mit platonischen Körpern

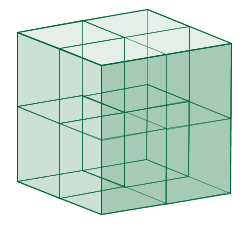
Mit Hexaedern (Würfeln) lässt  sich der dreidimensionale Raum vollständig ausfüllen, da die Kanten eines Hexaeders jeweils im rechten Winkel aufeinander stehen.

Bei den anderen vier platonischen Körpern kann jedoch nur eine Kombination von Oktaedern und Tetraedern mit jeweils gleich großen gleichseitigen Dreiecken als Seitenflächen den Raum ausfüllen.

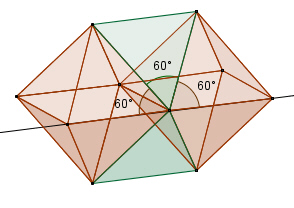
Da  die Innenwinkel im gleichseitigen Dreieck jeweils 60° betragen, stoßen bei einer Kombination Oktaeder – Tetraeder – Oktaeder jeweils drei 60°-Winkel an einem Eckpunkt zusammen, so dass die entsprechenden Kanten auf einer Geraden liegen.

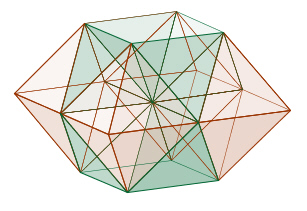
Insgesamt lässt sich durch eine abwechselnde Folge von Oktaedern und Tetraedern mit gleich großen gleichseitigen Dreiecken als Seitenflächen der dreidimensionale Raum vollständig ausfüllen.

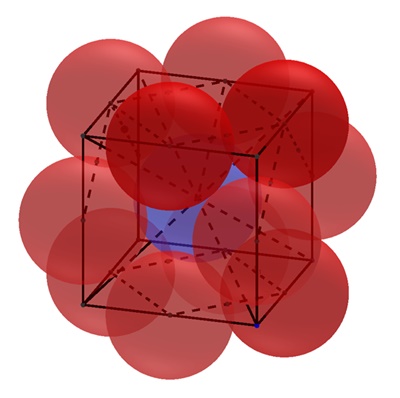
Würfel mit 13 Kugeln

Bei einem Würfel mit der Kantenlänge a berühren 12 gleichgroße Kugeln um die Kantenmittelpunkte mit dem Radius   jeweils ihre Nachbarkugeln.

Alle 12 Kugeln berühren eine gleich große (blaue) Kugel um den Würfelmittelpunkt.

               Schrägbild:                                                 Grundriss:

Geschichte – philosophische Bedeutung

Die Pythagoreer studierten bereits im 6. Jahrhundert v. Chr. die Eigenschaften regelmäßiger Körper.

Der griechische Philosoph Platon (ca. 427–347 v. Chr.), der sich ausführlich mit den fünf Körpern beschäftigte, wurde ihr Namensgeber.

Euklid (360–280 v. Chr.) bewies im XIII. Buch der Elemente, dass es genau fünf platonischen Körper gibt. 

Johannes Kepler schreibt in seinem Buch Harmonices Mundi (1619), S. 58:

„Das sind jene fünf Körper, die die Pythagoreer, Plato und Proklus, der Kommentator Euklids, die Weltfiguren zu nennen pflegten. . . . Nach Aristoteles ist es allgemeine Überzeugung, jene Philosophen hätten sich entsprechend der Fünfzahl dieser Figuren nach fünf einfachen Weltkörpern umgeschaut, nämlich nach den vier Elementen Luft, Wasser, Erde und der sogenannten Quintessenz oder Himmelsmaterie, indem sie die Eigenschaften der Figuren mit den Eigentümlichkeiten jener einfachen Körper in Zusammenhang brachten.“  (Übersetzung aus dem Lateinischen von Max Caspar, 1939)

Zuordnung der platonischen Körper zu den Elementen im Buch Harmonices Mundi von J. Kepler

           Erde                      Wasser                         Luft                          Feuer                Himmelsmaterie

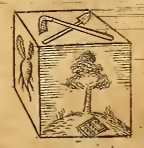
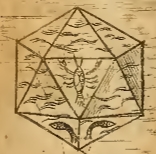
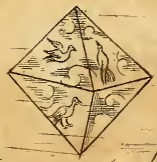
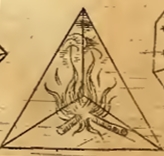
Das Keplersche Sphärenmodell

Aus Keplers Sicht war es kein Zufall, dass die Anzahl der fünf platonischen Körper um eins kleiner als die Anzahl der bekannten Planeten war. Er versuchte herauszufinden, ob die Abstände und Umlaufbahnen der Planeten von der Sonne durch Kugeln innerhalb dieser Polyeder definiert sind.

Er entwickelte ein Sphärenmodell, bei dem Merkur, Venus, Erde, Mars, Jupiter und Saturn kugelförmig ineinander geschachtelt sind durch Würfel, Tetraeder, Dodekaeder, Ikosaeder und Oktaeder mit der Sonne im Zentrum.

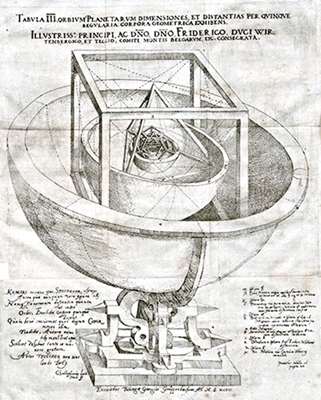
Keplers Sphärenmodell im Buch Mysterium Cosmographicum (1596)

Nach der Entdeckung weiterer Planeten (Uranus, Neptun) und nach genaueren Berechnungen
konnte das Sphärenmodell nicht mehr aufrecht erhalten werden und ist nur mehr historisch interessant.

Mobile mit den 5 platonischen Körper

Das Foto (M. Holzapfel) zeigt ein Mobile nach den Modellen von Doris Schattschneider und Wallace Walker,
die nach Bildvorlagen von M. C. Escher auf die platonischen Körper übertragen wurden. 

Die Abbildungen wurden mit GeoGebra erstellt. 

Quellen:  

http://de.wikipedia.org/wiki/Platonischer_Körper

http://www.3quarks.com/GIF-Animations/PlatonicSolids/index-de.html

Zurück
Zurück zur Startseite