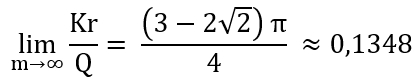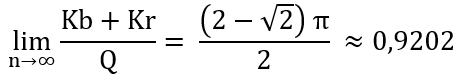Kreise in quadratischer Anordnung im Kreis

Der Radius des blauen Kreises sei a, des roten Kreises b und des Umfangskreises r.

Nach Pythagoras gilt in jedem Fall:  (a + b)² = 2 a² und damit b = a (√2 – 1)

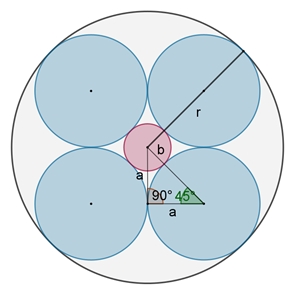
4 = 2² blaue Kreise:

r = 2a + b und b = a (√2 – 1), daraus folgt: r = a (√2 + 1)

a = r / (√2 + 1)  | Erweitern mit (√2 – 1)

a = r (√2 – 1)

Verhältnis der Flächeninhalte der blauen Kreise Kb zum Umfangskreis Ku:

Kb/Ku = 4 r² (√2 – 1)² π / (r² π) = 4 (√2 – 1)² ≈ 0,686

Verhältnis der Flächeninhalte der roten Kreise Kr zum Umfangskreis Ku mit b = r (√2 – 1)²

Kr/Ku = r² (√2 – 1)⁴ π / (r² π) = (√2 – 1) ⁴ ≈ 0,029

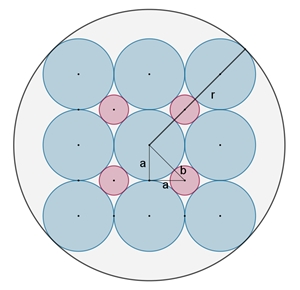
9 = 3² blaue Kreise:

r = 3a + 2b und b = a (√2 – 1), daraus folgt: r = a (2√2 + 1)

a = r (2√2 – 1)/7

Verhältnis der Flächeninhalte der blauen Kreise Kb zum Umfangskreis Ku:

Kb/Ku = 9 r² ((2√2 – 1)/7)² π / (r² π) = 9 ((2√2 – 1)/7)² ≈ 0,614

Verhältnis der Flächeninhalte der roten Kreise Kr zum Umfangskreis Ku:

b = r (√2 – 1) (2√2 – 1)/7 = r (5 – 3√2) / 7

Kr/Ku = 4 r² ((5 – 3√2) / 7)² π / (r² π) ≈ 0,047

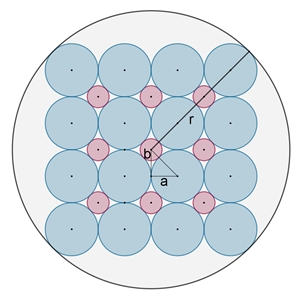
16 = 4² blaue Kreise:

r = 4a + 3b und b = a (√2 – 1), daraus folgt: r = a (3√2 + 1)

a = r (3√2 – 1)/17

Verhältnis der Flächeninhalte der blauen Kreise Kb zum Umfangskreis Ku:

Kb/Ku = 16 r² ((3√2 – 1)/17)² π / (r² π) = 16 ((3√2 – 1)/17)² ≈ 0,582

Verhältnis der Flächeninhalte der roten Kreise Kr zum Umfangskreis Ku:

b = r (√2 – 1) (3√2 – 1)/17

9 r² ((7 – 4√2)/17)² π / (r² π) ≈ 0,056

Für n² blaue Kreise gilt:

Kb/Ku = n²(((n – 1)√2 – 1)/(2٠(n – 1)² – 1))² = n² / (√2 n + 1 – √2)²

Für n gegen Unendlich geht das Verhältnis der Flächeninhalte der blauen Kreise zum Umfangskreis gegen 1/2.

Für m² rote Kreise (m = n – 1)  gilt:

Kr/Ku = m² ((√2 – 1)( m√2 – 1)/( 2 m² – 1))² = m² (3 – 2√2) / (√2 m + 1)²

Für das Verhältnis der Flächeninhalte der blauen und roten Kreise zusammen zum Umkreis gilt:

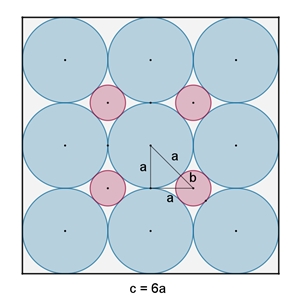
Kreise in quadratischer Anordnung im Quadrat

Der Radius des blauen Kreises sei a, des roten Kreises b und die Seitenlänge des umgrenzenden Quadrats c.

Nach Pythagoras gilt in jedem Fall:  (a + b)² = 2 a² und damit b = a (√2 – 1)

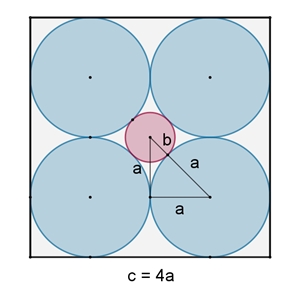
4 = 2² blaue Kreise:

Verhältnis der Flächeninhalte der blauen Kreise Kb zum Umfangsquadrat Q

Kb/Q = 4 a²π / (4a)² = π/4

Verhältnis der Flächeninhalte der roten Kreises Kr zum Umfangsquadrat Q

Kr/Q = a²(√2 – 1)² π / (4a)² = (3 – 2√2) π / 16 ≈ 0,0337

9 = 3² blaue Kreise:

Verhältnis der Flächeninhalte der blauen Kreise Kb zum Umfangsquadrat Q

Kb/Q = 9 a²π / (6a)² = π/4

Verhältnis der Flächeninhalte der roten Kreises Kr zum Umfangsquadrat Q

Kr/Q = 4 a²(√2 – 1)² π / (6a)² = (3 – 2√2) π / 9 ≈ 0,0599

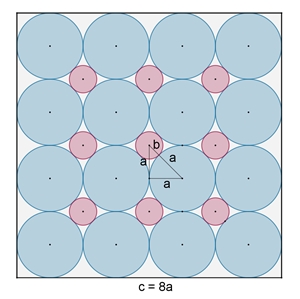
16 = 4² blaue Kreise:

Verhältnis der Flächeninhalte der blauen Kreise Kb zum Umfangsquadrat Q

Kb/Q = 16 a²π / (8a)² = π/4

Verhältnis der Flächeninhalte der roten Kreises Kr zum Umfangsquadrat Q

Kr/Q = 9 a²(√2 – 1)² π / (8a)² = 9 (3 – 2√2) π / 64 ≈ 0,0758

Für n² blaue Kreise gilt:

Kb/Ku = n² a²π /(2na)² = π/4

Das Verhältnis der Flächeninhalte der blauen Kreise Kb zum Umfangsquadrat Q bleibt konstant bei π/4.

Für m² rote Kreise (m = n – 1)  gilt:

Kr/Q = m² a²(√2 – 1)² π / (2(m+1)a)² = m² (3 – 2√2) /(4(m+1)²)

Verhältnis der Flächeninhalte der blauen und roten Kreise zusammen zum Umfangsquadrat Q