Spiralen

Eine Spirale ist eine ebene Kurve, die aus unendlich vielen Windungen um einen festen Punkt besteht und aus höchstens zwei Ästen zusammengesetzt ist, bei denen der Abstand vom Mittelpunkt vom Drehwinkel abhängt.

Spiralen kann man mathematisch durch Polarkoordinaten beschreiben, wobei gilt:

Der Radius r ist eine Funktion des Winkels φ:  r = r(φ)

In x-y-Koordinaten gilt dann: x = r(φ)٠cos(φ);  y = r(φ)٠sin(φ)

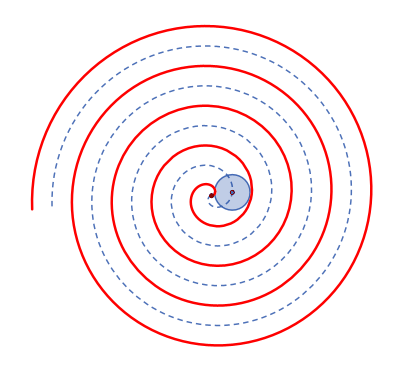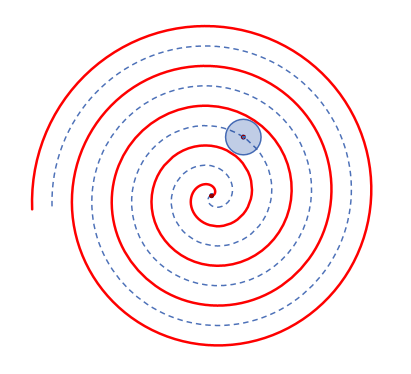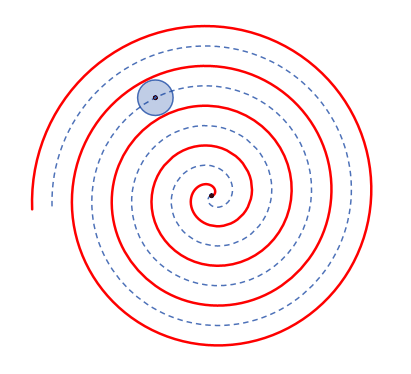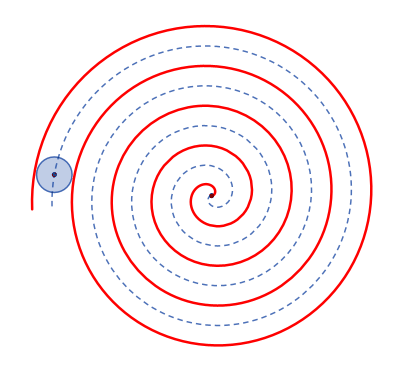
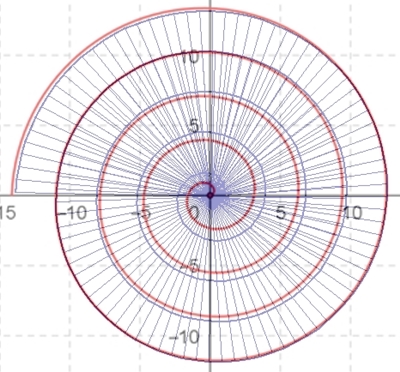
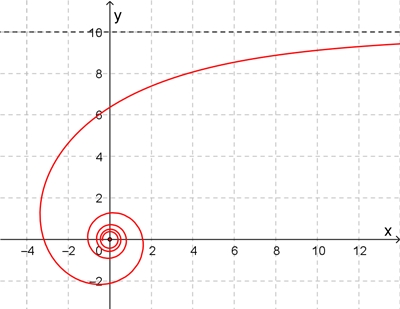
Die Kreisevolvente

In Polarkoordinaten:

In x-y-Koordinaten:

x = a cos(φ) + a φ sin(φ), y = a sin(φ) – a φ cos(φ)

a = 0,46; 0 ≦ φ ≦ 9,5 π

Bei der Kreisevolvente ist der Abstand der Spiralwindungen konstant.

Die archimedische Spirale

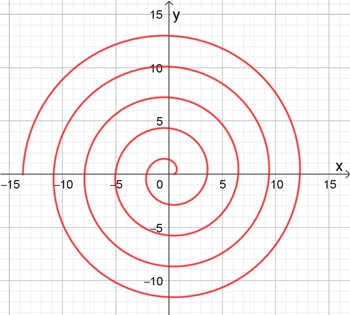
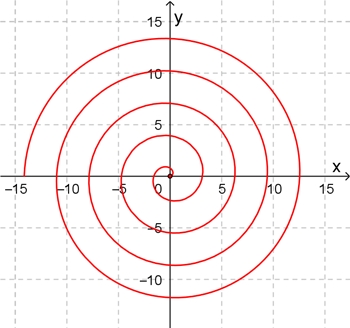
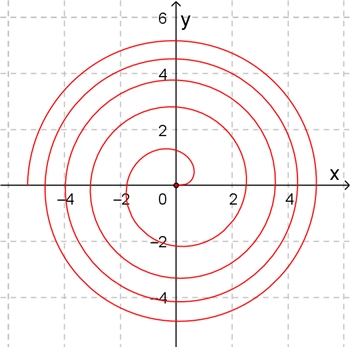
In Polarkoordinaten:  r(φ) = a φ

In x-y-Koordinaten: x = a φ cos(φ); y = a φ sin(φ)

a = 0,5; 0 ≦ φ ≦ 9π

Bei der Archimedischen Spirale ist der Abstand der Spiralwindungen nahezu konstant.

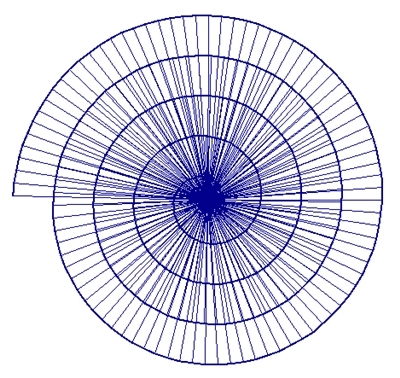
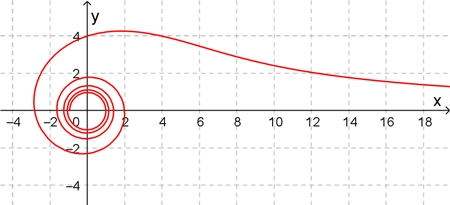
Die Wurzel-Spirale

Die Wurzelspirale lässt sich durch die Archimedische Spirale nähern, wobei gilt: Mit wachsender Windungszahl nähert sich die Wurzelspirale asymptotisch einer Archimedischen Spirale an.

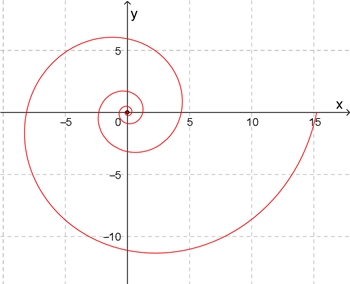
Die fermatsche oder parabolische Spirale

In Polarkoordinaten:  r(φ) = a

In x-y-Koordinaten: x = a  cos(φ); y = a  sin(φ)

a = 1; 0 ≦ φ ≦ 9π

Bei der fermatschen Spirale nimmt der Abstand der Spiralwindungen ab.

Die logarithmische Spirale

In Polarkoordinaten:  r(φ) = a exp(kφ)

In x-y-Koordinaten: x = a exp(kφ)  cos(φ); y = a exp(kφ)  sin(φ)

exp( ) = e^{( )},  e = 2,71828… (Eulersche Zahl)

a = 0,1; k = 0,2; 0 ≦ φ ≦ 8π

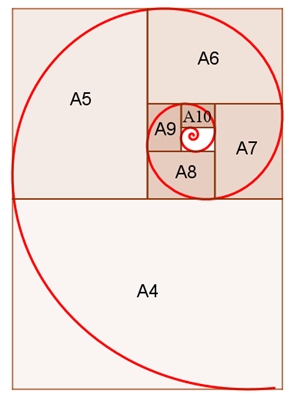
Spezialfall: goldene Spirale

k = 2 ln τ

siehe: goldener Schnitt – Konstruktionen

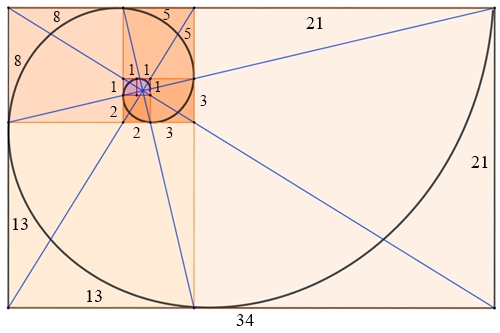
Wenn DIN-A-Rechtecke in Spiralform angeordnet werden,
lässt sich eine logarithmische Spirale einpassen.

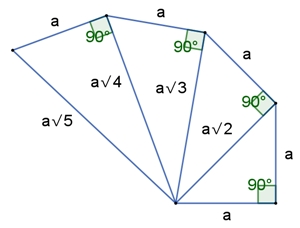
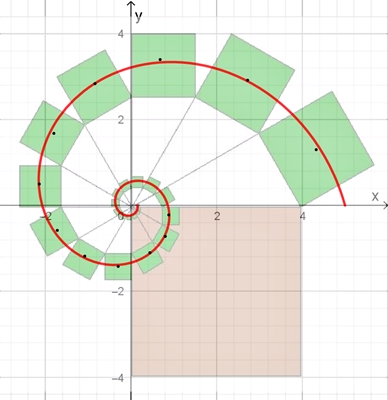
Die Pythagoras-Spirale

Die rechtwinkligen Dreiecke mit den grünen Quadraten sind ähnliche Dreiecke. Es gilt:

Die Summe der Flächeninhalte der grünen Quadrate ist gleich dem Flächeninhalt des braunen Quadrats.

Begründung s. Pythagoras

Logarithmische Spirale durch die Mittelpunkte der grünen Quadrate in Näherung:

x = a exp(kφ)  cos(φ)

y = a exp(kφ) sin(φ)

a = 0,148; k = 0,28

Die hyperbolische Spirale

In Polarkoordinaten:  r(φ) = a/φ

In x-y-Koordinaten: x = a/φ cos(φ); y = a/φ sin(φ)

a = 10; 0 < φ ≦ 9π

Für φ gegen 0 hat die hyperbolische Spirale als Asymptote y = a.

Für φ gegen unendlich hat die hyperbolische Spirale als Grenzwert den Nullpunkt (0; 0).

Die Lituus-Spirale

In Polarkoordinaten:  r(φ) = a /

In x-y-Koordinaten: x = a /  cos(φ); y = a /  sin(φ)

a = 5; 0 < φ ≦ 9π

Für φ gegen 0 hat die hyperbolische Spirale als Asymptote y = 0.

Für φ gegen unendlich hat die hyperbolische Spirale als Grenzwert den Nullpunkt (0; 0).

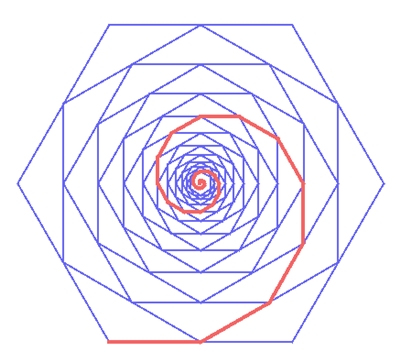
Kantenmittenspiralen bei regulären n-Ecken

In die Kantenmitten eines regelmäßigen n-Ecks wird wieder ein regelmäßiges n-Eck eingefügt, usw.

Die Verbindung aufeinanderfolgender Kantenmitten liefert eine eckige Spirale, die der logarithmischen Spirale entfernt ähnlich ist.

n = 6

n = 12

n = 18

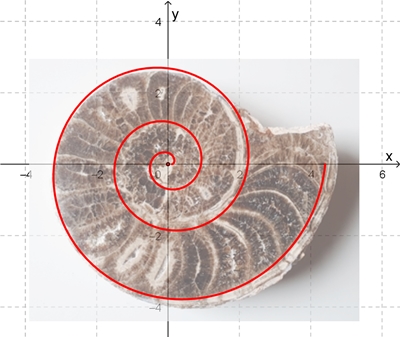
Querschnitt eines Ammoniten

Näherung der Spiralform in Polarkoordinaten:

r(φ) = a exp(b )

a = 0,11; b = 0,85; 0 ≦ φ ≦ 6π

Einfache spiralförmige Parkette

Mit dem gleichseitigen konkaven Fünfeck, Siebeneck und Neuneck als Parkettsteine lassen sich einfache spiralförmige Parkette erzeugen.

Parkettstein: jeweils konkaves

                      Fünfeck                                             Siebeneck                                              Neuneck

Siehe: Spiralförmige Parkette 

Ulam-Spirale

Mit blauer Farbe sind die Primzahlen dargestellt, mit gelber Farbe die geraden Quadratzahlen und mit rosa Farbe die ungeraden Quadratzahlen.

Siehe: Primzahlenmuster

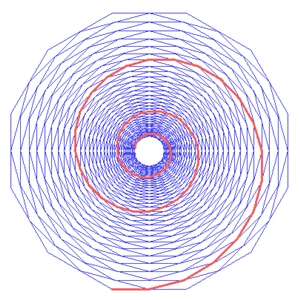
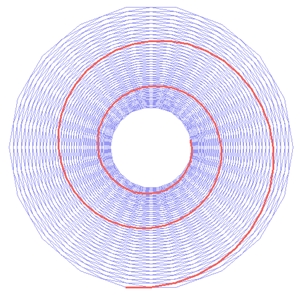
Spiralförmig wirkende zirkulare phasenverschobene Sinuskurven

Spiralförmige Parkette, siehe auch Spiral-Parkette