Das Dodekaeder

 

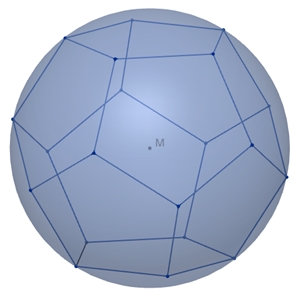
Das Dodekaeder hat als Oberfläche 12 kongruente reguläre Fünfecke, 30 gleich lange Kanten und 20 Ecken. Die Kantenlänge des Dodekaeders sei a.

Dodekaeder-Würfel-ani

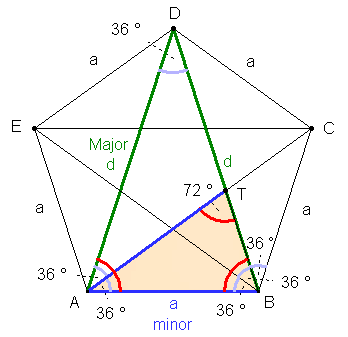
Der einbeschriebene Körper mit den Kantenlängen d stellt wegen seiner vierfachen Rotationssymmetrie im Dodekaeder einen Würfel dar.

Fünfeck-d

 

  

d : a = a : (d – a)
Daraus folgt für die Kantenlänge d, siehe goldener Schnitt, Konstruktionen:

d

 

 

 

  

Berechnung des Umkugelradius  des Dodekaeders

Dodekaeder-Würfel  
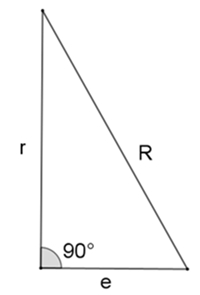 dode-fünfeckdode-dreieck


 
sin(36°) = a/2 / e
e = a / (2 sin(36°))
e,  d



Der Umkugelradius R ist die halbe Raumdiagonale des einbeschriebenen Würfels mit der Kantenlänge d:  R = d/2⸱√3

Umkugelradius R des Dodekaeders:  R = 1/4 (√3 + √15) a ≈ 1,401 a

Berechnung des Inkugelradius r des Dodekaeders:

r2 = R2 – e2  (Pythagoras)
r2 = 1/16 a2 (√3 + √15)2 – a2 (5 + √5)/10
r2 = a2 (11√5 + 25)/40

r = a/20 √(250 + 110 √5)   ≈ 1,1135 a

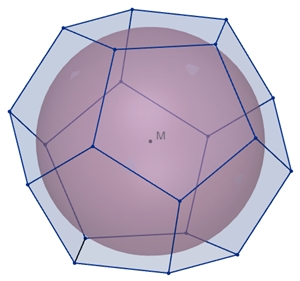
Inkugelradius r des Dodekaeders:  
r

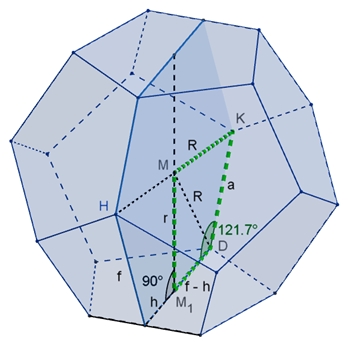
Dodekaeder mit Inkugel und Umkugel:

Inkugel          Umkugel

Berechnung des Oberflächeninhalts des Dodekaeders:

Der Oberflächeninhalt eines Dodekaeders ist der 12-fache Flächeninhalt eines regulären Fünfecks.

Flächeninhalt A eines regulären Fünfecks:

Fünfeck

   

A = 5 a h /2
tan(36°) = 1/2 a / h
h = a  / (2 tan(36°)) = a/10⸱√(25 + 10√5)  
Daraus folgt:
A = a2/4⸱√(25 + 10√5)

Oberflächeninhalt O des Dodekaeders mit O = 12 A:

O

 

Berechnung des Volumeninhalts des Dodekaeders:

Dodekaeder-Pyramide

 

Der Volumeninhalt eines Dodekaeders ist der 12-fache Volumeninhalt einer Pyramide aus regulärem Fünfeck mit Spitze M.

Volumeninhalt V5 der Pyramide ABCDEM:

V5 = 1/3 A h = 1/3⸱ a2/4⸱√(25 + 10√5)⸱ a/20 √(250 + 110√5)
V5 = 1/48 a3 (15 + 7√5)

Volumeninhalt V des Dodekaeders mit V = 12 V5 :

V = 1/4 (15 + 7√5) a3 ≈ 7,663 a3

 

 

Berechnung der Winkel im Dodekaeder:

Innenwinkel α des regulären Fünfecks α = 108° (= 3⸱180°/5).

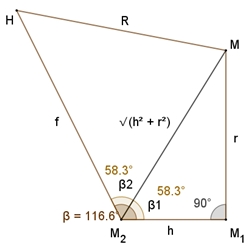
Berechnung des Winkels β zwischen benachbarten Flächen des Dodekaeders:

Dode-beta   dode-vierekck-1

f = e + h = 1/2⸱√(5 + 2√5) a  ≈  1,5388 a

tan(β1) = r / h = 1/20 √(250 + 110 √5) / (1/10 √(25 + 10√5)) = 1/2 (1 + √5)

β1 = 1/2 (135° -  arctan(1/3)) ≈ 58,283°

Mit Hilfe des Kosinussatzes, des Pythagoras und eines Computer-Algebra-Systems (CAS) lässt sich der Winkel β2 berechnen.
Es gilt: β2 = β1.

Daraus folgt:

β = β1 + β2 = 135° – arctan(1/3) ≈ 116,565°

Winkel β zwischen benachbarten Flächen:  β = 135° – arctan(1/3) ≈ 116,565°.

 

Berechnung des Winkels γ zwischen Kante und Fläche eines Dodekaeders:

Dode-gamma dode-viereck-2

  

 f – h = e = √((5+√5)/10) a ≈ 0,851 a

 

Berechnung von γ1:

tan(γ1) = r / e = 1/20 √(250 + 110 √5) / √((5+√5)/10) = 1/4 (3 + √5)
γ1 = arctan(1/4 (3 + √5)) ≈ 52,623°

 

 

  

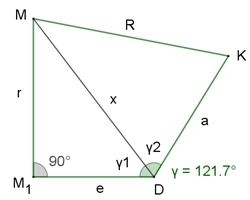
Berechnung von γ2:

x² = R² = e² + r² = (5+√5)/10 a² + (11√5 + 25)/40 a² = 1/8 (9 + 3√5) a²
x = R =  1/4 (√3 + √15) a

R² = R² + a² - 2aR cos(γ2)

2 R cos( γ2) = a

cos( γ2) = a / (2R)

cos( γ2) = 2/(√3 + √15) = 1/6 (√15 - √3)

γ2 = arccos(1/6 (√15 - √3)

γ2 = 90° - ½ arcsin(2/3)

γ2 = 69,095°

γ = γ1 + γ2 = 1/2 (225° + arctan(1/3)) ≈ 121,717°

Winkels γ zwischen Kante und Fläche:  γ = 1/2 (225° + arctan(1/3)) ≈ 121,717°

Zurück

Zurück zur Themenseite
Zurück zur Startseite